
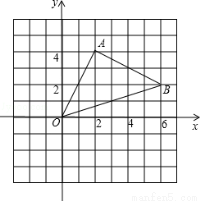
如图,△AOB中,A,B两点的坐标分别为(2,4)、(6,2),求:△AOB的面积.
(△AOB的面积可以看作一个长方形的面积减去一些小三角形的面积)
10.
【解析】
试题分析:作辅助线(过点A、B分别作x轴、y轴的垂线CE、CF交点为C,垂足分别为E、F)构建矩形ECFO.根据矩形的四个角都是直角的性质求得矩形的面积、矩形ECFO中△AEO、△ABC、△BFO的面积,从而求得S△AOB=SECFO﹣S△AOE﹣S△ACB﹣S△BOF.
试题解析:过点A、B分别作x轴、y轴的垂线CE、CF交点为C,垂足分别为E、F
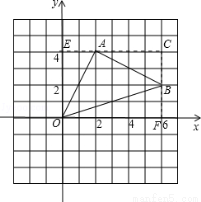
∵A(2,4)、B(6,2)
∴OE=AC=4,EA=CB=BF=2,OF=6,
∴S△AOB=SECFO﹣S△AOE﹣S△ACB﹣S△BOF= 6×4 =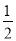 ×4×2
×4×2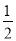 ×4×2=4
×4×2=4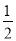 ×6×2=24﹣4﹣4﹣6=10 ,
×6×2=24﹣4﹣4﹣6=10 ,
∴△AOB的面积是10.
考点:1.三角形的面积2.坐标与图形性质.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源:2016届北京市七年级下学期期末数学试卷(解析版) 题型:选择题
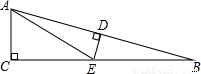
如图,在△ABC中,∠C=90°,∠B=15°,D是AB的中点,DE⊥AB于D,交BC于E,则∠CAE的度数是( )
A.15° B.30° C.60° D.75°
查看答案和解析>>
科目:初中数学 来源:2016届北京市七年级下学期期末数学试卷(解析版) 题型:选择题
如图:要测河岸相对两点A、B间距离,先从B出发与AB成90°角方向,向前走50米到C立一根标杆,然后方向不变继续朝前走50米到D处,在D处转90°沿DE方向走17米,到达E处,使A、C与E在同一直线上,那么测得A、B的距离为17米.这一作法的理论依据是( )
A.SSS B.SAS C.ASA D.AAS

查看答案和解析>>
科目:初中数学 来源:2015届黑龙江省八年级下学期期末考试数学试卷(解析版) 题型:解答题
计算:
(1)(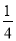 )﹣1﹣
)﹣1﹣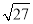 +(5﹣π)0
+(5﹣π)0
(2)(2x﹣1)2+(x﹣2)(x+2)﹣4x(x﹣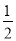 )
)
查看答案和解析>>
科目:初中数学 来源:2015届重庆市合川区第五学区八年级下学期半期考试数学试卷(解析版) 题型:选择题
若式子 有意义,则点P(a,b)在( )
有意义,则点P(a,b)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com