
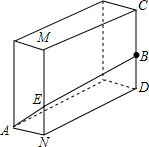
 如图,一块长方体砖宽AN=5cm,长ND=10cm,CD上的点B距地面的高BD=8cm,地面上A处的一只蚂蚁到B处吃食,需要爬行的最短路径是17cm.
如图,一块长方体砖宽AN=5cm,长ND=10cm,CD上的点B距地面的高BD=8cm,地面上A处的一只蚂蚁到B处吃食,需要爬行的最短路径是17cm. 分析 要求不在同一平面内的两点间的最短距离,首先要把两点所在的两个平面展开到一个平面内,然后根据题意确定数据,再根据勾股定理即可求解.
解答 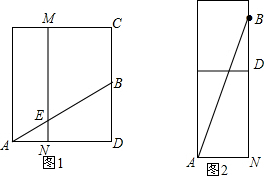 解:①如图1所示,连接AB,则AB的长即为A处到B处的最短路程.
解:①如图1所示,连接AB,则AB的长即为A处到B处的最短路程.
在Rt△ABD中,
∵AD=AN+DN=5+10=15cm,BD=8cm,
∴AB=$\sqrt{{AD}^{2}+{BD}^{2}}$=$\sqrt{{15}^{2}+{8}^{2}}$=17(cm).
②如图2所示,
AB=$\sqrt{{AN}^{2}+(DN+BD)^{2}}$=$\sqrt{{5}^{2}+{(10+8)}^{2}}$=$\sqrt{349}$(cm),
∵$\sqrt{349}$>17,
∴需要爬行的最短路径是17cm.
故答案为:17.
点评 本题的是平面展开-最短路径问题,解答此类问题时要先根据题意把立体图形展开成平面图形后,再确定两点之间的最短路径.一般情况是两点之间,线段最短.在平面图形上构造直角三角形解决问题.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
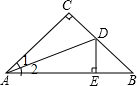 如图,在△ABC中,∠C=90°,AC=BC,AD是∠CAB的角平分线,DE⊥AB于点E,若AB=6cm,则△DEB的周长是( )
如图,在△ABC中,∠C=90°,AC=BC,AD是∠CAB的角平分线,DE⊥AB于点E,若AB=6cm,则△DEB的周长是( )| A. | 5cm | B. | 6cm | C. | 7cm | D. | 8cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
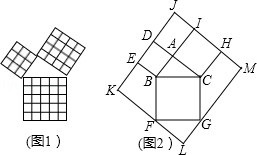 勾股定理被誉为“几何明珠”,在数学的发展历程中占有举足轻重的地位.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入长方形内得到的,∠BAC=90°,AB=3,AC=4,点D、E、F、G、H、I 都在长方形KLMJ的边上,则长方形KLMJ的面积为( )
勾股定理被誉为“几何明珠”,在数学的发展历程中占有举足轻重的地位.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入长方形内得到的,∠BAC=90°,AB=3,AC=4,点D、E、F、G、H、I 都在长方形KLMJ的边上,则长方形KLMJ的面积为( )| A. | 90 | B. | 100 | C. | 110 | D. | 121 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com