
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交BC的延长线于点M.
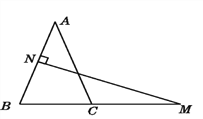
(1)若∠A=40°,求∠NMB的度数.
(2)如果将(1)中∠A的度数改为70°,其余条件不变,求∠NMB的度数.
(3)由(1)(2)你发现了什么规律?并说明理由.
【答案】(1) 20°;(2) 35°;
(3)规律:∠NMB=![]() ∠A.
∠A.
【解析】(1)根据等边对等角,由AB=AC可得到∠ABM=∠ACB,再结合已知∠A的度数,即可求出∠NMB的度数;
(2)仿照第(1)问的求解过程即可得到∠NMB的度数;
(3)结合上述两问的解答,即可发现∠NMB和∠A之间的大小关系,然后仿照上述解答过程进行验证即可.
解:(1)∵AB=AC,
∴∠ABM=∠ACB.
∵∠BAC=40°,∠ABM=∠ACB,
∴∠ABM=![]() ×(180°-∠BAC)=70°.
×(180°-∠BAC)=70°.
∵MN是AB的垂直平分线,∠ABM=70°,
∴∠NMB=90°-∠ABM=90°-70°=20°.
(2)与(1)同理可得∠B=![]() ×(180°-∠BAC)=55°,
×(180°-∠BAC)=55°,
∴∠NMB=90°-55°=35°.
(3)规律:在等腰△ABC中,当AB=AC,∠NMB的度数恰好为顶角∠A度数的一半,即∠NMB=![]() ∠A.理由如下:
∠A.理由如下:
∵AB=AC,
∴∠ABM=∠ACB.
∴∠ABM=![]() (180°-∠A)=90°-
(180°-∠A)=90°-![]() ∠A.
∠A.
∵∠ABM=90°-![]() ∠A,∠BNM=90°,
∠A,∠BNM=90°,
∴∠BMN=90°-∠ABM=![]() ∠A.
∠A.


科目:初中数学 来源: 题型:
【题目】如图,已知点A是双曲线y= ![]() 在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为斜边做等腰直角△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=
在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为斜边做等腰直角△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y= ![]() (k<0)上运动,则k的值是
(k<0)上运动,则k的值是 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于两个已知图形G1、G2,在G1上任取一点P,在G2上任取一点Q,当线段PQ的长度最小时,我们称这个最小长度为G1、G2的“密距”.例如,如上图,![]() ,
,![]() ,
,![]() ,则点A与射线OC之间的“密距”为
,则点A与射线OC之间的“密距”为![]() ,点B与射线OC之间的“密距”为3,如果直线y=x-1和双曲线
,点B与射线OC之间的“密距”为3,如果直线y=x-1和双曲线![]() 之间的“密距”为
之间的“密距”为![]() ,则k值为( )
,则k值为( )

A. k=4 B. k=-4 C. k=6 D. k=-6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.在平面直角坐标系中,点A(3,0),B(0,﹣4),C是x轴上一动点,过C作CD∥AB交y轴于点D.
(1)![]() 的值是 .
的值是 .
(2)若以A,B,C,D为顶点的四边形的面积等于54,求点C的坐标.
(3)将△AOB绕点A按顺时针方向旋转90°得到△AO′B′,设D的坐标为(0,n),当点D落在△AO′B′内部(包括边界)时,求n的取值范围.(直接写出答案即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,BC=12,∠B=30°,AB的垂直平分线DE交BC边于点E,AC的垂直平分线MN交BC于点N.
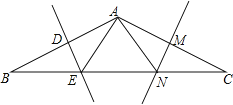
(1)求△AEN的周长;
(2)求证:BE=EN=NC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形纸片ABCD中,∠A=60°,将纸片折叠,点A、D分别落在A′、D′处,且A′D′经过B,EF为折痕,当D′F⊥CD时, ![]() 的值为 .
的值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学为备战省运会,在校运动队的学生中进行了全能选手的选拔,并将参加选拔学生的综合成绩分成四组,绘成了如下尚不完整的统计图表.
组别 | 成绩 | 组中值 | 频数 |
第一组 | 90≤x<100 | 95 | 4 |
第二组 | 80≤x<90 | 85 | m |
第三组 | 70≤x<80 | 75 | n |
第四组 | 60≤x<70 | 65 | 21 |
根据图表信息,回答下列问题:
(1)参加活动选拔的学生共有人;表中m= , n=;
(2)若将各组的组中值视为该组的平均值,请你估算参加选拔学生的平均成绩;
(3)将第一组中的4名学生记为A、B、C、D,由于这4名学生的体育综合水平相差不大,现决定随机挑选其中两名学生代表学校参赛,试通过画树形图或列表的方法求恰好选中A和B的概率. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有4个质地、大小均相同的小球,这些小球分别标有数字3,4,5,x.甲、乙两人每次同时从袋中各随机摸出1个球,并计算摸出的这2个小球上数字之和,记录后都将小球放回袋中搅匀,进行重复试验.实验数据如下表:
摸球总次数 | 10 | 20 | 30 | 60 | 90 | 120 | 180 | 240 | 330 | 450 |
“和为8”出现的频数 | 2 | 10 | 13 | 24 | 30 | 37 | 58 | 82 | 110 | 150 |
“和为8”出现的频率 | 0.20 | 0.50 | 0.43 | 0.40 | 0.33 | 0.31 | 0.32 | 0.34 | 0.33 | 0.33 |
解答下列问题:
(1)如果实验继续进行下去,根据上表数据,出现“和为8”的频率将稳定在它的概率附近.估计出现“和为8”的概率是;
(2)当x=7时,请用列表法或树状图法计算“和为8”的概率;并判断x=7是否可能.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com