练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．如图，将一长方形纸片沿EF折叠后，点DC分别落在点D′、C′的位置，若∠EFB=68°，则∠AED′=44°．

    分析 先根据两直线平行，内错角相等，由AD∥BC得到∠DEF=∠EFB=68°，再利用折叠的性质得到∠D′EF=∠DEF=68°，然后利用平角的定义求解．

    解答 解：∵AD∥BC，
    ∴∠DEF=∠EFB=68°，
    ∵长方形纸片沿EF折叠后，点DC分别落在点D′、C′的位置，
    ∴∠D′EF=∠DEF=68°，
    ∴∠∠AED′=180°-∠D′EF-∠DEF=180°-2×68°=44°．
    故答案为44°．

    点评 本题考查了平行线性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．也考查了折叠的性质．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    4．已知3x-2y=1，用含y的代数式表示x为（　　）
    A．x=$\frac{1+2y}{3}$B．x=$\frac{1-2y}{3}$C．y=$\frac{3x-1}{2}$D．y=$\frac{1-3x}{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．在一个盒子中装有红球、绿球、白球各1个，这3个球除颜色外其余都相同，小明先从盒子中摸出2个球后放回，小李再从盒子中摸出2个球．请用列表或画树状图法求他们摸到的4个球恰好包含所有颜色的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．燃灯佛舍利塔（简称燃灯塔）是通州八景之一，该塔始建于南北朝北周宇文时期，距今已有1300多年历史．燃灯塔距运河300米，是通州的象征．某同学想利用相似三角形的有关知识来求燃灯塔的高度．他先测量出燃灯塔落在地面上的影长为12米，然后在同一时刻立一根高2米的标杆，测得标杆影长为0.5米，那么燃灯塔高度为48m米．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．在△ABC中，∠A、∠B、∠C的度数比为4：5：6，那么△ABC是（　　）
    A．锐角三角形B．直角三角形C．钝角三角形D．等腰三角形

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．?ABCD的周长为60cm，其对角线交于O点，若△AOB的周长比△BOC的周长多10cm，则AB=20cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

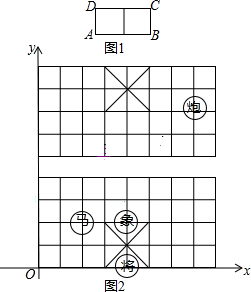    6．中国象棋中历来有“马”走“日”，“象”飞“田”之说，其意思是：在象棋棋盘上，“马”的走法如下：以“马”所在的位置为棋格所组成的任一“日”字的一个顶点，下一步“马”可以走到该“日”字与原位置相对的那个顶点，如图1马可以自A走到C（或自C走到A）也可自B走到D（或D走到B），在如图棋盘中，建立如图2所示直角坐标系：
    ①分别写出黑方“马”与红方“将”所在的点的坐标；
    ②根据“马”走“日”的行棋规则写出黑方“马”的下一步可能到达的所有可能点的坐标．
    ③若“马”与“将”成“日”字的对角位置时，称作捉“将”，那么黑方“马”至少要走几步才能捉“将”，用坐标写出其中一种行棋步骤．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．为得到二次函数y=-x2的图象，需将y=-x2+2x-2的图象（　　）
    A．向左平移2个单位，再向下平移2个单位
    B．向右平移2个单位，再向上平移2个单位
    C．向左平移1个单位，再向上平移1个单位
    D．向右平移1个单位，再向下平移1个单位

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．化简：$\frac{1}{a-b}$-$\frac{1}{a+b}$+$\frac{2b}{{a}^{2}+{b}^{2}}$-$\frac{4{b}^{3}}{{a}^{4}-{b}^{4}}$．

    查看答案和解析>>

    同步练习册答案