练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．在△ABC中，∠A、∠B、∠C的度数比为4：5：6，那么△ABC是（　　）
    A．锐角三角形B．直角三角形C．钝角三角形D．等腰三角形

    分析 已知三角形三个内角的度数之比，可以设一份为k°，根据三角形的内角和等于180°列方程求三个内角的度数，从而确定三角形的形状．

    解答 解：设一份为k°，则三个内角的度数分别为3k，4k，5k．
    则4k+5k+6k=180°，
    解得k=12，
    ∴4k=48，
    5k=60，
    6k=72，
    所以这个三角形是锐角三角形，
    故选：A．

    点评 此题主要考查三角形的内角和以及按边分类，直接根据三角形三个内角的度数比来判断是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

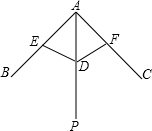    19．我国纸伞的制作工艺十分巧妙．如图，伞不管是张开还是收拢，伞柄AP始终平分同一平面内两条伞骨所成的角∠BAC，且AE=AF，DE=DF，从而保证伞圈能沿着伞柄滑动．有一种玩具伞张开时，BDC在同一直线上，若AB=50cm，AD=14cm，则制作一把这样的纸伞需要油纸的面积是（不记接缝）（　　）
    A．48cm2B．70πcm2C．2400πcm2D．2500πcm2

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

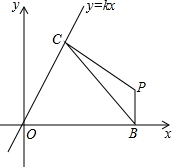    20．如图，已知平面直角坐标系中，直线y=kx（k≠0）经过点（a，$\sqrt{3}$a）（a＞0）．线段BC的两个端点分别在x轴与直线y=kx上（B、C均与原点O不重合）滑动，且BC=2，分别作BP⊥x轴，CP⊥直线y=kx，交点为P，经探究在整个滑动过程中，P、O两点间的距离为定值$\frac{4\sqrt{3}}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．北京市为了缓解交通拥堵问题，大力发展轨道交通．据调查，目前轨道交通日均运送乘客达到1320万人次．数据1320万用科学记数法表示正确的是（　　）
    A．132×101万B．13.2×102万C．1.32×103万D．1.32×104万

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．解不等式组$\left\{\begin{array}{l}5x-1＞3x-4\\ \frac{2}{3}-x≥-\frac{1}{3}\end{array}\right.$，并把不等式组的解集在数轴上表示出来．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．如图，将一长方形纸片沿EF折叠后，点DC分别落在点D′、C′的位置，若∠EFB=68°，则∠AED′=44°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．下列方程中是二元一次方程的是（　　）
    A．2x+y=6B．y2+x=1C．x2+3x+5=0D．$\frac{2}{x}$+x2+1=0

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

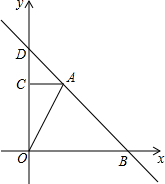    18．综合与探究：如图，在平面直角坐标系中，Rt△AOC的直角边OC在y轴正半轴上，且顶点O与坐标原点重合，点A的坐标为（2，4），直线y=-x+b过点A，与x轴交于点B．
    （1）求点B的坐标及直线AB的解析式；
    （2）动点P从点O出发，以每秒1个单位长的速度，沿O-C-A的路线向点A运动，同时动点M从点B出发，以相同的速度沿BO的方向向O运动，过点M作MQ⊥x轴，交线段BA或线段AO于点Q，当点P到达A点时，点P和点M都停止运动．在运动过程中，设动点P运动的时间为t秒．△APQ的面积为S，求S关于t的函数关系式；
    （3）是否存在以M、P、Q为顶点的三角形的面积与S相等？若存在，求t的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．某果品店经理预测某种水果能畅销，就用1200元购进这种水果，销售时果然供不应求，很快以每千克7元的价格出售，果品店又用1560元购进了第二批这种水果，但每千克的进价比第一批提高了20%，所购买的数量比第一批多20千克，当果品店以每千克8元的价格销售100千克后，因出现高温天气，水果不易保鲜，为减少损失，便以八折优惠价售完剩余的水果．
    （1）求第一批购进的这种水果的进价是每千克多少元？
    （2）该果品店在这两次销售中，总体上是盈利还是亏损？若亏损，亏损了多少？

    查看答案和解析>>

    同步练习册答案