
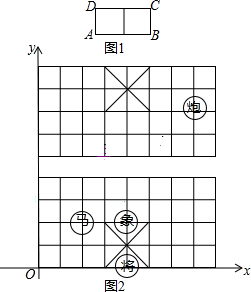
 中国象棋中历来有“马”走“日”,“象”飞“田”之说,其意思是:在象棋棋盘上,“马”的走法如下:以“马”所在的位置为棋格所组成的任一“日”字的一个顶点,下一步“马”可以走到该“日”字与原位置相对的那个顶点,如图1马可以自A走到C(或自C走到A)也可自B走到D(或D走到B),在如图棋盘中,建立如图2所示直角坐标系:
中国象棋中历来有“马”走“日”,“象”飞“田”之说,其意思是:在象棋棋盘上,“马”的走法如下:以“马”所在的位置为棋格所组成的任一“日”字的一个顶点,下一步“马”可以走到该“日”字与原位置相对的那个顶点,如图1马可以自A走到C(或自C走到A)也可自B走到D(或D走到B),在如图棋盘中,建立如图2所示直角坐标系:分析 ①根据点的坐标的意义写出“马”“将”所在的点的坐标;
②利用“马”走“日”的行棋规则,写出所有与点(2,2)成“日”字相对的点的坐标即可;
③利用“马”走“日”的行棋规则,可得到至少要走3步才能捉“将”,然后写出“马”所走过的点的坐标即可.
解答 解:①黑方“马”所在的点的坐标为(2,2);红方“将”所在的点的坐标为(4,0);
②黑方“马”的下一步可能到达的点的坐标为((0,1),(0,2),(1,0),(1,4),(3,0),(3,4),(4,1),(4,3);
③黑方“马”至少要走3步才能捉“将”,其中一种行棋步骤为(2,2)→(1,0)→(3,1)→(5,2).
点评 本题考查了坐标确定位置:平面内的点与有序实数对一一对应;记住直角坐标系中特殊位置点的坐标特征.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 132×101万 | B. | 13.2×102万 | C. | 1.32×103万 | D. | 1.32×104万 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
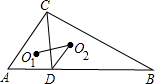 如图,△ABC中,CD⊥AB于D,O1、O2分别为△ACD和△BCD的内心,若AD=6,CD=8,BD=15,则cos∠O1O2D的值为$\frac{3\sqrt{13}}{13}$.
如图,△ABC中,CD⊥AB于D,O1、O2分别为△ACD和△BCD的内心,若AD=6,CD=8,BD=15,则cos∠O1O2D的值为$\frac{3\sqrt{13}}{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
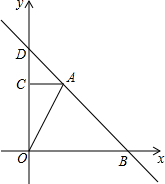 综合与探究:如图,在平面直角坐标系中,Rt△AOC的直角边OC在y轴正半轴上,且顶点O与坐标原点重合,点A的坐标为(2,4),直线y=-x+b过点A,与x轴交于点B.
综合与探究:如图,在平面直角坐标系中,Rt△AOC的直角边OC在y轴正半轴上,且顶点O与坐标原点重合,点A的坐标为(2,4),直线y=-x+b过点A,与x轴交于点B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com