
分析 (1)利用已知的等式类比得出an=$\frac{n+2}{n(n+1)×{2}^{n+1}}$=$\frac{1}{n×{2}^{n}}$-$\frac{1}{(n+1)×{2}^{n+1}}$;
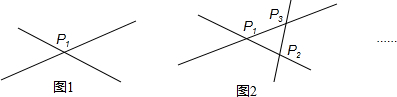
(2)①4条直线两两相交,最多有1+2+3=6个交点;
②n条直线两两相交,最多有1+2+3+…+n-1=$\frac{1}{2}$n(n-1)个交点;由此代入求得答案即可.
解答 解:(1)an=$\frac{n+2}{n(n+1)×{2}^{n+1}}$=$\frac{1}{n×{2}^{n}}$-$\frac{1}{(n+1)×{2}^{n+1}}$;
(2)①4条直线两两相交,最多有6个交点;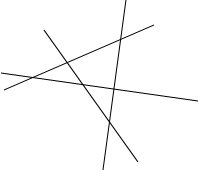
②1+2+3+…+99=$\frac{1}{2}$×99×(99+1)=4950.
答:100条直线两两相交时,最多能找到4950个交点.
点评 本题考查了图形的变化规律,是一道关于数字猜想的问题,关键是通过归纳与总结,得到其中的规律解决问题.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:解答题
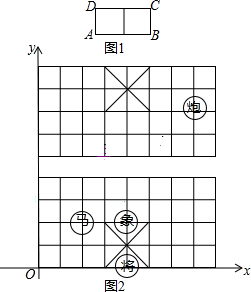 中国象棋中历来有“马”走“日”,“象”飞“田”之说,其意思是:在象棋棋盘上,“马”的走法如下:以“马”所在的位置为棋格所组成的任一“日”字的一个顶点,下一步“马”可以走到该“日”字与原位置相对的那个顶点,如图1马可以自A走到C(或自C走到A)也可自B走到D(或D走到B),在如图棋盘中,建立如图2所示直角坐标系:
中国象棋中历来有“马”走“日”,“象”飞“田”之说,其意思是:在象棋棋盘上,“马”的走法如下:以“马”所在的位置为棋格所组成的任一“日”字的一个顶点,下一步“马”可以走到该“日”字与原位置相对的那个顶点,如图1马可以自A走到C(或自C走到A)也可自B走到D(或D走到B),在如图棋盘中,建立如图2所示直角坐标系:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (5,-3) | B. | (3,-5) | C. | (-5,3) | D. | (-3,5) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com