
【题目】如图,△ABC中,∠A=30°,∠B=62°,CE平分∠ACB,CD⊥AB于D,DF⊥CE于F,求∠CDF的度数.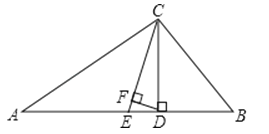
【答案】解:∵∠A=40°,∠B=72°,
∴∠ACB=180°﹣(∠A+∠B),
=180°﹣(30°+62°),
=180°﹣92°,
=88°,
∵CE平分∠ACB,
∴∠ECB=![]() ∠ACB=44°,
∠ACB=44°,
∵CD⊥AB于D,
∴∠CDB=90°,
∴∠BCD=90°﹣∠B=90°﹣62°=28°,
∴∠ECD=∠ECB﹣∠BCD=44°﹣28°=16°,
∵DF⊥CE于F,
∴∠CFD=90°,
∴∠CDF=90°﹣∠ECD=90°﹣16°=74°.
【解析】首先根据三角形的内角和定理求得∠ACB的度数,以及∠BCD的度数,根据角的平分线的定义求得∠BCE的度数,则∠ECD可以求解,然后在△CDF中,利用内角和定理即可求得∠CDF的度数.
【考点精析】本题主要考查了三角形三边关系的相关知识点,需要掌握三角形两边之和大于第三边;三角形两边之差小于第三边;不符合定理的三条线段,不能组成三角形的三边才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图1,平面直角坐标系x0y中,点A(0,2),B(1,0),C(﹣4,0)点D为射线AC上一动点,连结BD,交y轴于点F,⊙M是△ABD的外接圆,过点D的切线交x轴于点E.
(1)判断△ABC的形状;
(2)当点D在线段AC上时,
①证明:△CDE∽△ABF;
②如图2,⊙M与y轴的另一交点为N,连结DN、BN,当四边形ABND为矩形时,求tan∠DBC;
(3)点D在射线AC运动过程中,若![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图四边形ABCD中,AD=DC,∠DAB=∠ACB=90°,过点D作DF⊥AC,垂足为F.DF与AB相交于E.设AB=15,BC=9,P是射线DF上的动点.当△BCP的周长最小时,DP的长为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一枚运载火箭从地面O处发射,当火箭到达A点时,从地面C处的雷达站测得AC的距离是6km,仰角是43°,1s后,火箭到达B点,此时测得仰角为45.5°,这枚火箭从点A到点B的平均速度是多少?(结果精确到0.01)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解方程:x2﹣4x+2=0,下列配方正确的是( )
A.(x﹣2)2=2
B.(x+2)2=2
C.(x﹣2)2=﹣2
D.(x﹣2)2=6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com