
 在正方形ABCD中,AB=8,M是DC上的一点,且DM=2,N是AC上的一动点,求|AN-MN|的最小值与最大值.
在正方形ABCD中,AB=8,M是DC上的一点,且DM=2,N是AC上的一动点,求|AN-MN|的最小值与最大值.| AD2+DM2 |
| 82+22 |
| 17 |
| 17 |


科目:初中数学 来源: 题型:
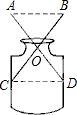 小红家有一个小口瓶(如图所示),她很想知道它的内径是多少?但是尺子不能伸到里边直接测,于是她拿来了两根长度相同的细木条,并且把两根细木条的中点固定在一起,木条可以绕中点转动,这样只要量出AB的长,就可以知道玻璃瓶的内径是多少,那么△OAB≌△OCD理由是( )
小红家有一个小口瓶(如图所示),她很想知道它的内径是多少?但是尺子不能伸到里边直接测,于是她拿来了两根长度相同的细木条,并且把两根细木条的中点固定在一起,木条可以绕中点转动,这样只要量出AB的长,就可以知道玻璃瓶的内径是多少,那么△OAB≌△OCD理由是( )| A、边角边 | B、角边角 |
| C、边边边 | D、角角边 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com