
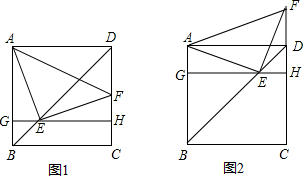
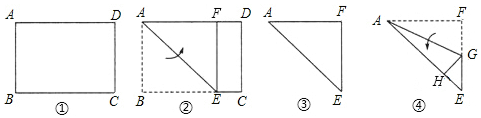
分析 (1)根据四边形ABCD是正方形,BD是对角线,且GH∥BC,求证△GEB和△HDE都是等腰直角三角形.又利用EF⊥AE,可得∠EFH=∠AEG,然后即可求证△AGE≌△EHF,推出AE=EF即可解决问题;
(2)分两种情况进行讨论:(i)当点E运动到BD的中点时,利用四边形AFHG是矩形,可得S四边形AFHG=$\frac{1}{2}$;
(ii)当点E不在BD的中点时,点E在运动(与点B、D不重合)的过程中,四边形AFHG是直角梯形.由(1)知,△AGE≌△EHF,同理,图(2),△AGE≌△EHF可得,S四边形AFHG=$\frac{1}{2}$(FH+AG)•GH=$\frac{1}{2}$,然后即可得出结论.
解答 解:(1)∵四边形ABCD是正方形,BD是对角线,且GH∥BC,
∴四边形AGHD和四边形GHCB都是矩形,
△GEB和△HDE都是等腰直角三角形.
∴∠AGE=∠EHF=90°,GH=BC=AB,EG=BG
∴GH-EG=AB-BG
即EH=AG
∴∠EFH+∠FEH=90°
又∵EF⊥AE,
∴∠AEG+∠FEH=90°.
∴∠EFH=∠AEG
∴△AGE≌△EHF
∴AE=EF,∵∠AEF=90°,
∴△AEF是等腰直角三角形.
(2)四边形AFHG的面积没有发生变化.
(i)当点E运动到BD的中点时,
四边形AFHG是矩形,S四边形AFHG=$\frac{1}{2}$.
(ii)当点E不在BD的中点时,点E在运动(与点B、D不重合)的过程中,四边形AFHG是直角梯形.
由(1)知,△AGE≌△EHF
同理,图(2),△AGE≌△EHF
∴FH=EG=BG.
∴FH+AG=BG+AG=AB=1
这时,S四边形AFHG=$\frac{1}{2}$(FH+AG)•GH=$\frac{1}{2}$.
综合(i)、(ii)可知四边形AFHG的面积没有发生改变,都是 $\frac{1}{2}$.
点评 此题主要考查正方形的性质,全等三角形的判定与性质等知识点的理解和掌握,此题有一定的拔高难度,属于难题.


科目:初中数学 来源: 题型:填空题
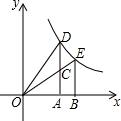 如图,在平面直角坐标系中,点D的函数y=$\frac{k}{x}$(x>0)的图象上,DA垂直x轴于点A,点C为线段AD的中心,延长线段OC交函数y=$\frac{k}{x}$(x>0)的图象于点E,EB垂直x轴于点B,若直角梯形ABEC的面积为1,则k的值为4.
如图,在平面直角坐标系中,点D的函数y=$\frac{k}{x}$(x>0)的图象上,DA垂直x轴于点A,点C为线段AD的中心,延长线段OC交函数y=$\frac{k}{x}$(x>0)的图象于点E,EB垂直x轴于点B,若直角梯形ABEC的面积为1,则k的值为4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
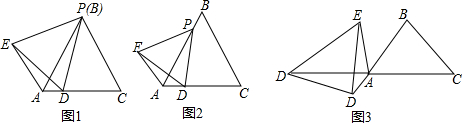
 一艘轮船位于灯塔P南偏西60°方向上的点A处,在A正东方向上距离20海里的有一点B处,在灯塔P南偏西45°方向上,求A距离灯塔P的距离.
一艘轮船位于灯塔P南偏西60°方向上的点A处,在A正东方向上距离20海里的有一点B处,在灯塔P南偏西45°方向上,求A距离灯塔P的距离.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
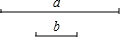 在数学课上,老师提出如下问题:
在数学课上,老师提出如下问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$-1 | B. | $\sqrt{2}$+1 | C. | $\frac{2}{3}$ | D. | $\frac{\sqrt{2}+1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com