
 一艘轮船位于灯塔P南偏西60°方向上的点A处,在A正东方向上距离20海里的有一点B处,在灯塔P南偏西45°方向上,求A距离灯塔P的距离.
一艘轮船位于灯塔P南偏西60°方向上的点A处,在A正东方向上距离20海里的有一点B处,在灯塔P南偏西45°方向上,求A距离灯塔P的距离.分析 易知△PBC为等腰直角三角形,可得BC=PC,设BC=PC=x,则AC=20+x,在Rt△APC中,根据tan∠APC=$\frac{AC}{PC}$,可得$\frac{20+x}{x}$=$\sqrt{3}$,推出x=10($\sqrt{3}$+1)(海里).在Rt△APC中,由∠A=30°,可得PA=2PC,由此即可解决问题.
解答 解:如图,AC⊥PC,∠APC=60°,∠BPC=45°,AB=20,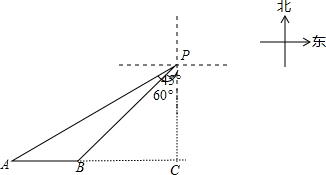
在△PBC中,∵∠BPC=45°,
∴△PBC为等腰直角三角形,
∴BC=PC,设BC=PC=x,则AC=20+x,
在Rt△APC中,∵tan∠APC=$\frac{AC}{PC}$,
∴$\frac{20+x}{x}$=$\sqrt{3}$,
∴x=10($\sqrt{3}$+1)(海里).
在Rt△APC中,∵∠A=30°,
∴PA=2PC=20($\sqrt{3}$+1)≈54.6(海里)
答:A距离灯塔P的距离为54.6海里.
点评 本题考查了解直角三角形的应用-方向角:在辨别方向角问题中:一般是以第一个方向为始边向另一个方向旋转相应度数.在解决有关方向角的问题中,一般要根据题意理清图形中各角的关系,有时所给的方向角并不一定在直角三角形中,需要用到两直线平行内错角相等或一个角的余角等知识转化为所需要的角.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:解答题
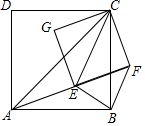 如图,四边形ABCD,和四边形CFEG都是正方形,连接AC、AE、BF、CE.
如图,四边形ABCD,和四边形CFEG都是正方形,连接AC、AE、BF、CE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
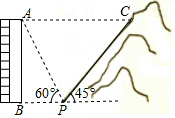 图,一居民楼底部B与山脚P位于同一水平线上,小李在P处测得居民楼顶A的仰角为60°,然后他从P处沿坡角为45°的山坡向上走到C处,这时,PC=30m,点C与点A恰好在同一水平线上,点A、B、P、C在同一平面内.
图,一居民楼底部B与山脚P位于同一水平线上,小李在P处测得居民楼顶A的仰角为60°,然后他从P处沿坡角为45°的山坡向上走到C处,这时,PC=30m,点C与点A恰好在同一水平线上,点A、B、P、C在同一平面内.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
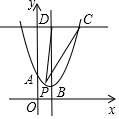 如图,在平面直角坐标系中,点A在y轴上,点A、B($\frac{3}{2}$,m)、C(3,n)均在抛物线y=(x-1)2+1上,点D在抛物线的对称轴上,CD∥x轴.若点P为抛物线上A、B两点间任意一点(包括点A、B),则△PCD面积S的取值范围是3≤S≤$\frac{15}{4}$.
如图,在平面直角坐标系中,点A在y轴上,点A、B($\frac{3}{2}$,m)、C(3,n)均在抛物线y=(x-1)2+1上,点D在抛物线的对称轴上,CD∥x轴.若点P为抛物线上A、B两点间任意一点(包括点A、B),则△PCD面积S的取值范围是3≤S≤$\frac{15}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com