
【题目】如图,![]() ,⊙
,⊙![]() 是Rt△
是Rt△![]() 的内切圆,分别切
的内切圆,分别切![]() 于点
于点![]() ,连接
,连接![]() .
.![]() 的延长线交
的延长线交![]() 于点
于点![]() ,
,![]() .
.
(1)求证:四边形![]() 为正方形;
为正方形;
(2)求⊙![]() 的半径;
的半径;
(3)求![]() 的长.
的长.
【答案】(1)、证明过程见解析;(2)、1.5;(3)、7.5
【解析】试题分析:(1)根据内接圆得出矩形,然后根据OE=OF得出正方形;(2)根据正方形得出△OED∽△ACD,从而得出半径;(3)根据内切圆得出DE=0.5,设BD=c,则DE=x+0.5,根据AG=AF=4.5则AB=5+x,根据勾股定理求出AB的长度.
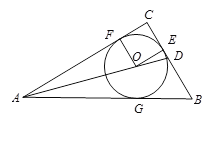
试题解析:(1)因为⊙O是Rt△ABC的内接圆,分别切BC,AC,AB 于点E,F,G
∴∠CFO=∠OEC=90°
∵∠C=90°.∴则四边形OECF为 矩形,
又∵OE="OF=r" ∴四边形OECF为 正方形
(2)由四边形OECF为 正方形
∴OE//AC ,CE=CF=r
∴△OED∽△ACD
∴![]()
∴![]()
解得:r=![]()
(3)⊙![]() 是Rt△
是Rt△![]() 的内切圆,由(2)得DE=
的内切圆,由(2)得DE=![]() ,设BD=x,则BE=BG=x+
,设BD=x,则BE=BG=x+![]()
∵AG=AF=![]() ,∴AB="5+x" ,
,∴AB="5+x" ,
由![]() 得
得![]()
解得:x=![]()
∴AB =![]()


 作业辅导系列答案
作业辅导系列答案科目:初中数学 来源: 题型:
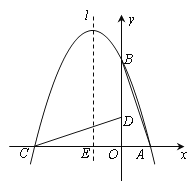
【题目】如图,在直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC.抛物线y=ax2+bx+c经过点A、B、C.
(1)求抛物线的解析式.
(2)若点P是第二象限内抛物线上的动点,其横坐标为t.
①设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求出当△CEF与△COD相似时点P的坐标.
![]() ②是否存在一点P,使△PCD的面积最大?若存在,求出△PCD面积的最大值;若不存在,请说明理由.
②是否存在一点P,使△PCD的面积最大?若存在,求出△PCD面积的最大值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com