
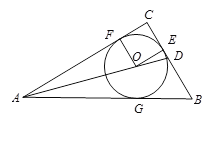
ЁОЬтФПЁПШчЭМЃЌдкжБНЧзјБъЯЕжагавЛжБНЧШ§НЧаЮAOBЃЌOЮЊзјБъдЕуЃЌOA=1ЃЌtanЁЯBAO=3ЃЌНЋДЫШ§НЧаЮШЦдЕуOФцЪБеыа§зЊ90ЁуЃЌЕУЕНЁїDOCЃЎХзЮяЯпy=ax2+bx+cОЙ§ЕуAЁЂBЁЂCЃЎ
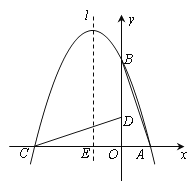
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЎ
ЃЈ2ЃЉШєЕуPЪЧЕкЖўЯѓЯоФкХзЮяЯпЩЯЕФЖЏЕуЃЌЦфКсзјБъЮЊtЃЎ
ЂйЩшХзЮяЯпЖдГЦжсlгыxжсНЛгквЛЕуEЃЌСЌНгPEЃЌНЛCDгкFЃЌЧѓГіЕБЁїCEFгыЁїCODЯрЫЦЪБЕуPЕФзјБъЃЎ
![]() ЂкЪЧЗёДцдквЛЕуPЃЌЪЙЁїPCDЕФУцЛ§зюДѓЃПШєДцдкЃЌЧѓГіЁїPCDУцЛ§ЕФзюДѓжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЂкЪЧЗёДцдквЛЕуPЃЌЪЙЁїPCDЕФУцЛ§зюДѓЃПШєДцдкЃЌЧѓГіЁїPCDУцЛ§ЕФзюДѓжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ ХзЮяЯпЕФНтЮіЪНЮЊy=-x2-2x+3ЃЛЃЈ2ЃЉ ЂйЃЈ-1ЃЌ4ЃЉЛђЃЈ-2ЃЌ3ЃЉЃЛЂк![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉЯШЧѓГіAЁЂBЁЂCЕФзјБъЃЌдйдЫгУД§ЖЈЯЕЪ§ЗЈОЭПЩвджБНгЧѓГіЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЂйгЩЃЈ1ЃЉЕФНтЮіЪНПЩвдЧѓГіХзЮяЯпЕФЖдГЦжсЃЌЗжРрЬжТлЕБЁЯCEF=90ЁуЪБЃЌЕБЁЯCFE=90ЁуЪБЃЌИљОнЯрЫЦШ§НЧаЮЕФаджЪОЭПЩвдЧѓГіPЕуЕФзјБъЃЛ
ЂкЯШдЫгУД§ЖЈЯЕЪ§ЗЈЧѓГіжБЯпCDЕФНтЮіЪНЃЌЩшPMгыCDЕФНЛЕуЮЊNЃЌИљОнCDЕФНтЮіЪНБэЪОГіЕуNЕФзјБъЃЌдйИљОнSЁїPCD=SЁїPCN+SЁїPDNОЭПЩвдБэЪОГіШ§НЧаЮPCDЕФУцЛ§ЃЌдЫгУЖЅЕуЪНОЭПЩвдЧѓГіНсТлЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉдкRtЁїAOBжаЃЌOA=1ЃЌtanЁЯBAO=![]() =3ЃЌ
=3ЃЌ
ЁрOB=3OA=3ЃЎ
ЁпЁїDOCЪЧгЩЁїAOBШЦЕуOФцЪБеыа§зЊ90ЁуЖјЕУЕНЕФЃЌ
ЁрЁїDOCЁеЁїAOBЃЌ
ЁрOC=OB=3ЃЌOD=OA=1ЃЌ
ЁрAЁЂBЁЂCЕФзјБъЗжБ№ЮЊЃЈ1ЃЌ0ЃЉЃЌЃЈ0ЃЌ3ЃЉЃЈ-3ЃЌ0ЃЉЃЎ
ДњШыНтЮіЪНЮЊ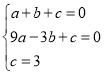 ЃЌНтЕУЃК
ЃЌНтЕУЃК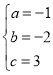 ЃЎ
ЃЎ
ЁрХзЮяЯпЕФНтЮіЪНЮЊy=-x2-2x+3ЃЛ
ЃЈ2ЃЉЂйЁпХзЮяЯпЕФНтЮіЪНЮЊy=-x2-2x+3ЃЌ
ЁрЖдГЦжсl=-![]() =-1ЃЌ
=-1ЃЌ
ЁрEЕуЕФзјБъЮЊЃЈ-1ЃЌ0ЃЉЃЎ
ШчЭМЃЌЕБЁЯCEF=90ЁуЪБЃЌЁїCEFЁзЁїCODЃЎДЫЪБЕуPдкЖдГЦжсЩЯЃЌМДЕуPЮЊХзЮяЯпЕФЖЅЕуЃЌPЃЈ-1ЃЌ4ЃЉЃЛ
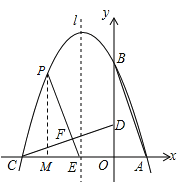
ЕБЁЯCFE=90ЁуЪБЃЌЁїCFEЁзЁїCODЃЌЙ§ЕуPзїPMЁЭxжсгкЕуMЃЌдђЁїEFCЁзЁїEMPЃЎ
Ёр![]() ЃЌ
ЃЌ
ЁрMP=3EMЃЎ
ЁпPЕФКсзјБъЮЊtЃЌ
ЁрPЃЈtЃЌ-t2-2t+3ЃЉЃЎ
ЁпPдкЕкЖўЯѓЯоЃЌ
ЁрPM=-t2-2t+3ЃЌEM=-1-tЃЌ
Ёр-t2-2t+3=-ЃЈt-1ЃЉЃЈt+3ЃЉЃЌ
НтЕУЃКt1=-2ЃЌt2=-3ЃЈвђЮЊPгыCжиКЯЃЌЫљвдЩсШЅЃЉЃЌ
Ёрt=-2ЪБЃЌy=-ЃЈ-2ЃЉ2-2ЁСЃЈ-2ЃЉ+3=3ЃЎ
ЁрPЃЈ-2ЃЌ3ЃЉЃЎ
ЁрЕБЁїCEFгыЁїCODЯрЫЦЪБЃЌPЕуЕФзјБъЮЊЃКЃЈ-1ЃЌ4ЃЉЛђЃЈ-2ЃЌ3ЃЉЃЛ
ЂкЩшжБЯпCDЕФНтЮіЪНЮЊy=kx+bЃЌгЩЬтвтЃЌЕУ
![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
ЁржБЯпCDЕФНтЮіЪНЮЊЃКy=![]() x+1ЃЎ
x+1ЃЎ
ЩшPMгыCDЕФНЛЕуЮЊNЃЌдђЕуNЕФзјБъЮЊЃЈtЃЌ![]() t+1ЃЉЃЌ
t+1ЃЉЃЌ
ЁрNM=![]() t+1ЃЎ
t+1ЃЎ
ЁрPN=PM-NM=-t2-2t+3-ЃЈ![]() t+1ЃЉ=-t2-
t+1ЃЉ=-t2-![]() t+2ЃЎ
t+2ЃЎ
ЁпSЁїPCD=SЁїPCN+SЁїPDNЃЌ
ЁрSЁїPCD=![]() PN
PN![]() CM+
CM+![]() PN
PN![]() OM
OM
=![]() PNЃЈCM+OMЃЉ
PNЃЈCM+OMЃЉ
=![]() PN
PN![]() OC
OC
=![]() ЁС3ЃЈ-t2-
ЁС3ЃЈ-t2-![]() t+2ЃЉ
t+2ЃЉ
=-![]() ЃЈt+
ЃЈt+![]() ЃЉ2+
ЃЉ2+![]() ЃЌ
ЃЌ
ЁрЕБt=-![]() ЪБЃЌSЁїPCDЕФзюДѓжЕЮЊ
ЪБЃЌSЁїPCDЕФзюДѓжЕЮЊ![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП ЖЫЮчНкГдєезгЪБжаЛЊУёзхЕФДЋЭГЯАЙпЃЎЮхдТГѕЮхдчГПЃЌаЁРіЕФТшТшгУВЛЭИУїзАзХвЛаЉєезгЃЈєезгГ§ФкВПЯкСЯВЛЭЌЭтЃЌЦфЫћвЛЧаЯрЭЌЃЉЃЌЦфжаЯуГІЯкєезгСНИіЃЌЛЙгавЛаЉТЬЖЙЯкєезгЃЌЯжаЁРіДгжаШЮвтФУГівЛИіЪЧЯуГІЯкєезгЕФИХТЪЮЊ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓДќзгжаТЬЖЙЯкєезгЕФИіЪ§ЃЛ
ЃЈ2ЃЉаЁРіЕквЛДЮШЮвтФУГівЛИієезгЃЈВЛЗХЛиЃЉЃЌЕкЖўДЮдйФУГівЛИієезгЃЌЧыФугУЪїаЮЭМЛђСаБэЗЈЃЌЧѓаЁРіСНДЮФУЕНЕФЖМЪЧТЬЖЙЯкєезгЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() ,Ёб
,Ёб![]() ЪЧRtЁї
ЪЧRtЁї![]() ЕФФкЧадВЃЌЗжБ№Ча
ЕФФкЧадВЃЌЗжБ№Ча![]() гкЕу
гкЕу![]() ,СЌНг
,СЌНг![]() .
.![]() ЕФбгГЄЯпНЛ
ЕФбгГЄЯпНЛ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() .
.
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮ![]() ЮЊе§ЗНаЮЃЛ
ЮЊе§ЗНаЮЃЛ
ЃЈ2ЃЉЧѓЁб![]() ЕФАыОЖЃЛ
ЕФАыОЖЃЛ
ЃЈ3ЃЉЧѓ![]() ЕФГЄ.
ЕФГЄ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаУќЬтжаЃЌецУќЬтЪЧ( )
A. ШЮКЮЪ§ЕФСуДЮУнЖМЕШгк1
B. ЖдНЧЯпЯрЕШЧвДЙжБЕФЫФБпаЮЪЧе§ЗНаЮ
C. гавЛЬѕБпЯрЕШЕФСНИіЕШбќжБНЧШ§НЧаЮШЋЕШ
D. гаСНЬѕжБНЧБпЖдгІЯрЕШЕФСНИіжБНЧШ§НЧаЮШЋЕШ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвдЯТЮЪЬтЃЌВЛЪЪКЯГщбљЕїВщЕФЪЧЃЈЁЁЁЁЃЉ
A. СЫНтШЋЪажааЁбЇЩњЕФУПЬьЕФСуЛЈЧЎ B. ТУПЭЩЯИпЬњСаГЕЧАЕФАВМь
C. ЕїВщФГХњДЮЦћГЕЕФПЙзВЛїФмСІ D. ЕїВщФГГиЬСжаВнгуЕФЪ§СП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
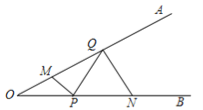
ЁОЬтФПЁПШчЭМЃЌЁЯAOBЃН30ЁуЃЌЕуMЁЂNЗжБ№дкБпOAЁЂOBЩЯЃЌЧвOMЃН1ЃЌONЃН4ЃЌЕуPЁЂQЗжБ№дкБпOBЁЂOAЩЯЃЌдђMPЃЋPQЃЋQNЕФзюаЁжЕЪЧ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаУќЬтжаЃЌМйУќЬтЪЧЃЈ ЃЉ
A.НЧЦНЗжЯпЩЯШЮвтвЛЕуЕННЧСНБпЕФОрРыЯрЕШB.ШЋЕШШ§НЧаЮЕФЖдгІНЧЯрЕШ
C.ЫФИіНЧЖМЯрЕШЕФСтаЮЪЧе§ЗНаЮD.гавЛИіНЧЪЧжБНЧЕФЫФБпаЮЪЧОиаЮ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com