
【题目】如图,已知正方形ABCD的边长为6,E是BC中点,将正方形边CD沿DE折叠到DF,将AD折叠,使AD与DF重合,折痕交AB于G,连接BF,CF,现在有如下4个结论:①G、F、E三点共线;②BG=4;③△BEF∽△CDF;④S△BFG=![]() .
.
在以上4个结论中,正确的有 ________________(填番号).

科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以M,N为圆心,大于 ![]() MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;④S△DAC:S△ABC=1:3.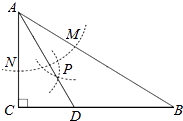
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,BD平分∠ABC交AC于D,DE⊥AB于E,若DE=1cm,∠CBD=30°,求∠A的度数和AC的长. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰三角形ABC中,AB=AC,以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系,抛物线y=﹣![]() x2+
x2+![]() x+4经过A、B两点.
x+4经过A、B两点.

(1)写出点A、点B的坐标;
(2)若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移,分别交线段OA、CA和抛物线于点E、M和点P,连接PA、PB.设直线l移动的时间为t(0<t<4)秒,求四边形PBCA的面积S(面积单位)与t(秒)的函数关系式,并求出四边形PBCA的最大面积;
(3)在(2)的条件下,是否存在t,使得△PAM是直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2014年全国两会民生活题再次成为社会焦点,央视记者为了了解百姓“两会民生话题”的聚焦点,随机调查了部分北京市民,并对结果进行整理.绘制了如下不完整的统计图表.
组别 | 焦点话题 | 人数 |
A | 食品安全 | 80 |
B | 教育医疗 | M |
C | 就业养老 | 100 |
D | 生态环保 | 120 |
E | 其它 | 60 |
请根据图表中提供的信息解答下列问题:
(1)填空:这次调查的样本容量是 ,m= ;扇形统计图中,E组所对圆心角的度数为 .
(2)北京市现常驻人口数达2000万,请估计关注D组话题的市民人数
(3)若在这次接受调查的市民中,随机抽查一人,则此人关注C组话题的概率是 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=ax+b的图象经过点(1,2),点(﹣1,6),且与x轴交于点B,与y轴交于点A. 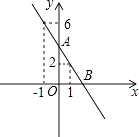
(1)求出这个一次函数的解析式;
(2)求出一次函数图象与两坐标轴围成的图形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com