
【题目】如图,在等边△ABC中,AB=10,BD=4,BE=2,点P从点E出发沿EA方向运动,连结PD,以PD为边,在PD的右侧按如图所示的方式作等边△DPF,当点P从点E运动到点A时,点F运动的路径长是________.

【答案】8
【解析】
作FG⊥BC于点G,DE’⊥AB于点E’,易证E点和E’点重合,则∠FGD=∠DEP=90°;由∠EDB+∠PDF=90°可知∠EDP+∠GFD=90°,则易得∠EPD=∠GDF,再由PD=DF易证△EPD≌△GDF,则可得FG=DE,故F点的运动轨迹为平行于BC的线段,据此可进行求解.
解:作FG⊥BC于点G,DE’⊥AB于点E’,由BD=4、BE=2与∠B=60°可知DE⊥AB,即∠
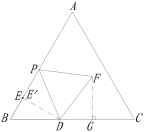
∵DE’⊥AB,∠B=60°,
∴BE’=BD×![]() =2,
=2,
∴E点和E’点重合,
∴∠EDB=30°,
∴∠EDB+∠PDF=90°,
∴∠EDP+∠GFD=90°=∠EDP+∠DPE,
∴∠DPE=∠GFD
∵∠DEP=∠FGD=90°,FD=GP,
∴△EPD≌△GDF,
∴FG=DE,DG=PE,
∴F点运动的路径与G点运动的路径平行,即与BC平行,
由图可知,当P点在E点时,G点与D点重合,
∵DG=PE,
∴F点运动的距离与P点运动的距离相同,
∴F点运动的路径长为:AB-BE=10-2=8,
故答案为:8.


科目:初中数学 来源: 题型:
【题目】如图,已知直线y=![]() x与双曲线y=
x与双曲线y=![]() 交于A、B两点,且点A的横坐标为
交于A、B两点,且点A的横坐标为![]() .
.
(1)求k的值;
(2)若双曲线y=![]() 上点C的纵坐标为3,求△AOC的面积;
上点C的纵坐标为3,求△AOC的面积;
(3)在坐标轴上有一点M,在直线AB上有一点P,在双曲线y=![]() 上有一点N,若以O、M、P、N为顶点的四边形是有一组对角为60°的菱形,请写出所有满足条件的点P的坐标.
上有一点N,若以O、M、P、N为顶点的四边形是有一组对角为60°的菱形,请写出所有满足条件的点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,李老师出示了如下框中的题目.
在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,如图.试确定线段AE与DB的大小关系,并说明理由. |
|
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:
AE DB(填“>”,“<”或“=”).

图1 图2
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”).
理由如下:如图2,过点E作EF∥BC,交AC于点F.
(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求CD的长(请你直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,线段AB和射线BM交于点B.
(1)利用尺规完成以下作图,并保留作图痕迹(不写作法)
①在射线BM上作一点C,使AC=AB;
②作∠ABM 的角平分线交AC于D点;
③在射线CM上作一点E,使CE=CD,连接DE.

(2)在(1)所作的图形中,猜想线段BD与DE的数量关系,并证明之.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数的图象经过点![]() .
.
![]() 写出函数表达式;
写出函数表达式;
![]() 这个函数的图象在哪几个象限?
这个函数的图象在哪几个象限?![]() 随
随![]() 的增大怎样变化?
的增大怎样变化?
![]() 点
点![]() 、
、![]() 在这个函数的图象上吗?
在这个函数的图象上吗?
![]() 如果点
如果点![]() 在图象上,求
在图象上,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足,下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=EF=EC;④AE=EC,其中正确的是________(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 与
与![]() 有公共顶点
有公共顶点![]() (顶点均按逆时针排列),
(顶点均按逆时针排列),![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,连接
的中点,连接![]() 并延长交直线
并延长交直线![]() 于点
于点![]() ,连接
,连接![]() .
.
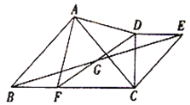
(1)如图,当![]() 时,
时,
求证:①![]() ;
;
②![]() 是等腰直角三角形.
是等腰直角三角形.
(2)当![]() 时,画出相应的图形(画一个即可),并直接指出
时,画出相应的图形(画一个即可),并直接指出![]() 是何种特殊三角形.
是何种特殊三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用适当的方法解方程:
(1)25 y 2- 16 = 0; (2)y 2+ 2 y-99=0;
(3)3x 2 + 2x -3=0; (4)(2x + 1)2 =3(2x + 1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD.
(1)求证:△ACE≌△ACF;
(2)若AB=21,AD=9,AC=17,求CF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com