
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:填空题
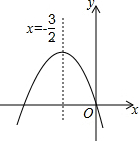 如图,已知二次函数y=ax2+bx+c的图象如图所示,给出以下四个结论:①abc=0;②a+b+c>0;③a>b;④4ac-b2<0.其中正确结论有①③④.
如图,已知二次函数y=ax2+bx+c的图象如图所示,给出以下四个结论:①abc=0;②a+b+c>0;③a>b;④4ac-b2<0.其中正确结论有①③④.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a>2016 | B. | a<2016 | C. | a>505 | D. | a<505 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
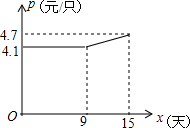 某企业接到一批茶杯生产任务,按要求在15天内完成,预定这批茶杯的出厂价为每个6元,为按时完成任务,该企业招收了新工人,设新工人小王第x天生产的茶杯数量为y个,y与x满足如下关系:y=$\left\{\begin{array}{l}{54x(0≤x≤5)}\\{30x+120(5<x≤15)}\end{array}\right.$.
某企业接到一批茶杯生产任务,按要求在15天内完成,预定这批茶杯的出厂价为每个6元,为按时完成任务,该企业招收了新工人,设新工人小王第x天生产的茶杯数量为y个,y与x满足如下关系:y=$\left\{\begin{array}{l}{54x(0≤x≤5)}\\{30x+120(5<x≤15)}\end{array}\right.$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
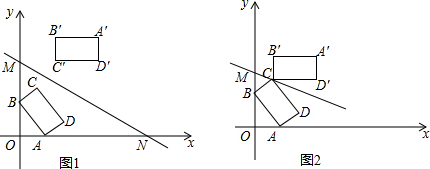
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
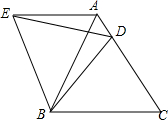 在等边三角形△ABC中,BC=6,点D是边AC上动点(点D与点A,C不重合),连接BD,将BD绕点B逆时针旋转60°得到BE,连接BD,AE.
在等边三角形△ABC中,BC=6,点D是边AC上动点(点D与点A,C不重合),连接BD,将BD绕点B逆时针旋转60°得到BE,连接BD,AE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com