
����Ŀ����ͼ����![]() �Ƕ����߶�
�Ƕ����߶�![]() ��һ�㣬
��һ�㣬![]() ��
��![]() ����ֱ�ӵ�
����ֱ�ӵ�![]() ��
��![]() ������1����/�룬2����/����ٶ���ֱ��
������1����/�룬2����/����ٶ���ֱ��![]() �����˶�����
�����˶�����![]() ���߶�
���߶�![]() �ϣ���
�ϣ���![]() ���߶�
���߶�![]() �ϣ���
�ϣ���
��1������![]() ��
��![]() �˶�����һʱ��ʱ������
�˶�����һʱ��ʱ������![]() ����˵����
����˵����![]() ���߶�
���߶�![]() �ϵ�λ�ã�
�ϵ�λ�ã�
��2���ڣ�1���������£���![]() ��ֱ��
��ֱ��![]() ��һ�㣬��
��һ�㣬��![]() ����
����![]() ��ֵ��
��ֵ��
��3���ڣ�1���������£�����![]() ��
��![]() �˶�5���ǡ����
�˶�5���ǡ����![]() ����ʱ��
����ʱ��![]() ֹͣ�˶�����
ֹͣ�˶�����![]() �����˶�����
�����˶�����![]() ���߶�
���߶�![]() �ϣ�����
�ϣ�����![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() ���е㣬���н��ۣ���
���е㣬���н��ۣ���![]() ��ֵ���䣻��
��ֵ���䣻��![]() ��ֵ���䣮����˵����ֻ��һ����������ȷ�ģ������ҳ���ȷ�Ľ��۲���ֵ��
��ֵ���䣮����˵����ֻ��һ����������ȷ�ģ������ҳ���ȷ�Ľ��۲���ֵ��
![]()
���𰸡���1����P���߶�AB��![]() ������2��
������2��![]() ��
��![]() ����3�����ۢ�
����3�����ۢ�![]() ��ֵ������ȷ��
��ֵ������ȷ��![]() .
.
��������
��1�����˶�ʱ��Ϊt�룬�ú�t�Ĵ���ʽ�ɱ�ʾ���߶�PD��AC��������![]() ����֪��
����֪��![]() ���߶�
���߶�![]() �ϵ�λ�ã�
�ϵ�λ�ã�
��2����![]() ��֪
��֪![]() ������Q���߶�AB��ʱ�����������ɵ�
������Q���߶�AB��ʱ�����������ɵ�![]() ���ٽ��
���ٽ��![]() �ɵ�
�ɵ�![]() ��ֵ������Q���߶�AB���ӳ�����ʱ���ɵ�
��ֵ������Q���߶�AB���ӳ�����ʱ���ɵ�![]() ����
����![]() ��ֵ.
��ֵ.
��3����![]() ֹͣ�˶�ʱ��
ֹͣ�˶�ʱ��![]() �������CM��AB��������ϵ����PM��PN��ֵ���Ժ�AB��ʽ������ʾ���ɵ�MN��AB��������ϵ����֪
�������CM��AB��������ϵ����PM��PN��ֵ���Ժ�AB��ʽ������ʾ���ɵ�MN��AB��������ϵ����֪![]() ��ֵ.
��ֵ.
�⣺��1�����˶�ʱ��Ϊt�룬��![]() ��
��
��![]() ��
��![]() ����
����![]()
![]() ��
��![]() ��
��![]() ����
����![]()
���Ե�P���߶�AB��![]() ����
����
��2������ͼ������Q���߶�AB��ʱ��
![]()
��![]() ��֪
��֪![]() ��
��
![]()
![]()
![]()
����ͼ������Q���߶�AB���ӳ�����ʱ��
![]()
![]() ��
��![]()
![]()
![]()
�ۺ�������![]() ��ֵΪ
��ֵΪ![]() ��
��![]() ��
��
��3����![]() ��ֵ����.
��ֵ����.
�ɵ�![]() ��
��![]() �˶�5��ɵ�
�˶�5��ɵ�![]() ��
��
��ͼ������M��N�ڵ�Pͬ��ʱ��
![]()
��![]() ֹͣ�˶�ʱ��
ֹͣ�˶�ʱ��![]() ��
��
![]() ��
��![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() ���е㣬
���е㣬
![]()
![]()
![]()
![]()
![]()
![]()
����Cֹͣ�˶�����D�����˶�ʱ��MN��ֵ���䣬����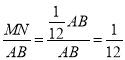 ��
��
��ͼ������M��N�ڵ�P���ʱ��
![]()
��![]() ֹͣ�˶�ʱ��
ֹͣ�˶�ʱ��![]() ��
��
![]() ��
��![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() ���е㣬
���е㣬
![]()
![]()
![]()
![]()
![]()
![]()
����Cֹͣ�˶�����D�����˶�ʱ��MN��ֵ���䣬����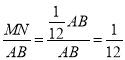 ��
��
���Ԣ�![]() ��ֵ������ȷ��
��ֵ������ȷ��![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ�� AB�������ύ���![]() �� ����P��·��
�� ����P��·��![]() �˶�.
�˶�.

(1)��ֱ��AB�ı���ʽ;
(2)����P��OB�ϣ�ʹ��APƽ��![]() ʱ�����ʱ��P������;
ʱ�����ʱ��P������;
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У���C����B��AEƽ�֡�BAC��FΪ����AE��һ�㣨�����E�غϣ�����FD��BC��D��
��1�������F���A�غϣ��ҡ�C=50�㣬��B=30������ͼ1�����EFD�Ķ�����
��2�������F���߶�AE�ϣ������A�غϣ�����ͼ2���ʡ�EFD���C����B��������������ϵ����˵�����ɣ�
��3�������F����ABC�ⲿ����ͼ3����ʱ��EFD���C����B��������ϵ�Ƿ�ᷢ���仯����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC��ֱ������ϵ�У�
��1�����ѡ�ABC����ƽ��2����λ��������ƽ��1����λ�õ���A1B1C1��������A1B1C1����д����A1��B1��C1�����ꣻ
��2�����ABC�������
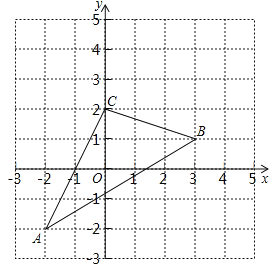
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ��
��![]() ��
��![]() ������ͬһ��ֱ���ϣ�
������ͬһ��ֱ���ϣ�![]() ƽ��
ƽ��![]() ��
��![]() ƽ��
ƽ��![]() .
.
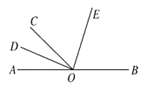
��1����![]() ����
����![]() ��
��
��2����![]() ����
����![]() ��
��
��3��![]() �Ƿ���
�Ƿ���![]() �Ķ����ı仯���仯��������䣬�����Ƕ��٣�����˵�����ɣ�����仯����˵����α仯.
�Ķ����ı仯���仯��������䣬�����Ƕ��٣�����˵�����ɣ�����仯����˵����α仯.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ijѧУ�������飬A��ѧ���ﹲ��������B��ѧ������������˽�ҳ��ȣ�C��ѧ�����У�D��ѧ���������������ݵ����������˲�������ͳ��ͼ��
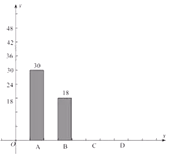
���� | Ƶ�� | Ƶ�� |
A | 30 |
|
B | 18 | 0.15 |
C |
| 0.40 |
D |
|
|
��1��ѧ����________�ˣ� ![]() ________��
________�� ![]() ________��
________��
��2����ȫ����ͳ��ͼ��
��3������У����2000�ˣ��ﹲ����������________�ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Ҫ�õ�AB��CD��ֻ��Ҫ����һ������������������������� ��

A. ��1����3 B. ��B����BCD��180��
C. ��2����4 D. ��D����BAD��180��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
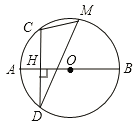
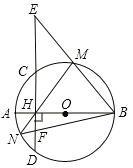
����Ŀ����ͼ���߶�AB �ǡ�O��ֱ������CD��AB�ڵ�H����M�ǻ�CBD ������һ�㣬AH=2��CH=4��
��1�����O �İ뾶r �ij��ȣ�
��2����sin��CMD��
��3��ֱ��BM��ֱ��CD�ڵ�E��ֱ��MH����O �ڵ� N������BN��CE�ڵ� F����HE![]() HF��ֵ��
HF��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
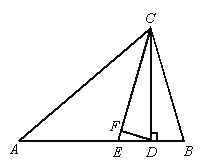
����Ŀ����ͼ����ABC�У���A=30������B=70����CEƽ�֡�ACB��CD��AB��D��DF��CE��F��
(1)��˵��CD����CBE�Ľ�ƽ���ߣ�
(2)�͡�B��ȵĽ��� ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com