练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，△ACE是以□ABCD的对角线AC为边的等边三角形，点C与点E关于x轴对称.若E点的坐标是（7，－3 ），则D点的坐标是 ( )

    A.(4,0)
    B.( ,0)
    C.(5,0)
    D.( ,0)

    【答案】C
    【解析】试题解析：如图，

    ∵点C与点E关于x轴对称，E点的坐标是（7，-3 ），
    ∴C的坐标为（7，3 ），
    ∴CH=3 ，CE=6 ，
    ∵△ACE是以ABCD的对角线AC为边的等边三角形，
    ∴AC=6 ，
    ∴AH=9，
    ∵OH=7，
    ∴AO=DH=2，
    ∴OD=5，
    ∴D点的坐标是（5，0），
    所以答案是（5，0）．
    【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识，掌握平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】英国曼彻斯特大学的两位科学家因为成功地从石墨中分离出石墨烯，荣获了诺贝尔物理学奖.石墨烯的理论厚度仅0.000 000 000 34米，将这个数用科学记数法表示为（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线与x轴交于A、B两点，与y轴交于点C，且OA=2，OC=3．

    （1）求抛物线的解析式；

    （2）作Rt△OBC的高OD，延长OD与抛物线在第一象限内交于点E，求点E的坐标；

    （3）①在x轴上方的抛物线上，是否存在一点P，使四边形OBEP是平行四边形？若存在，求出点P的坐标；若不存在，请说明理由；

    ②在抛物线的对称轴上，是否存在上点Q，使得△BEQ的周长最小？若存在，求出点Q的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】【探索新知】
    已知平面上有n（n为大于或等于2的正整数）个点A1 ， A2 ， A3 ， …An ， 从第1个点A1开始沿直线滑动到另一个点，且同时满足以下三个条件：①每次滑动的距离都尽可能最大；②n次滑动将每个点全部到达一次；③滑动n次后必须回到第1个点A1 ， 我们称此滑动为“完美运动”，且称所有点为“完美运动”的滑动点，记完成n个点的“完美运动”的路程之和为Sn ．
    （1）如图1，滑动点是边长为a的等边三角形三个顶点，此时S3=；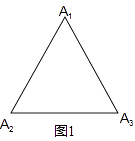

    （2）如图2，滑动点是边长为a，对角线（线段A1A2、A2A4）长为b的正方形四个顶点，此时S4= ．
    【深入研究】
    现有n个点恰好在同一直线上，相邻两点距离都为1，

    （3）如图3，当n=3时，直线上的点分别为A1、A2、A3 ．
    为了完成“完美运动”，滑动的步骤给出如图4所示的两种方法：
    方法1：A1→A3→A2→A1 ， 方法2：A1→A2→A3→A1 ．
    ①其中正确的方法为 ．
    A．方法1 B．方法2 C．方法1和方法2
    ②完成此“完美运动”的S3= ．


    （4）当n分别取4，5时，对应的S4= ， S5=
    （5）若直线上有n个点，请用含n的代数式表示Sn ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，小红将一张直角梯形纸片沿虚线剪开，得到矩形和三角形两张纸片，测得AB=15，AD=12．在进行如下操作时遇到了下面的几个问题，请你帮助解决．

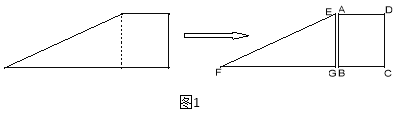
    （1）将△EFG的顶点G移到矩形的顶点B处，再将三角形绕点B顺时针旋转使E点落在CD边上，此时，EF恰好经过点A（如图2）求FB的长度

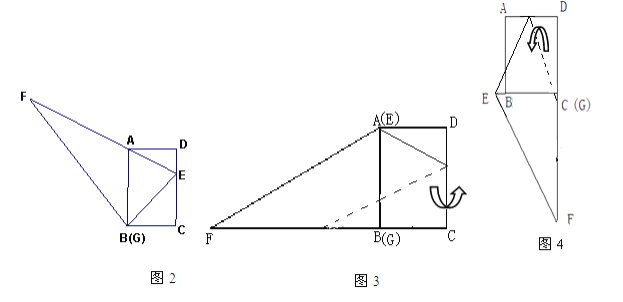
    （2）在（1）的条件下，小红想用△EFG包裹矩形ABCD,她想了两种包裹的方法如图3、图4，请问哪种包裹纸片的方法使得未包裹住的面积大？（纸片厚度忽略不计）请你通过计算说服小红。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】恺桐超市购进一批四阶魔方，按进价提高40%后标价，为了让利于民，增加销量，超市决定打八折出售，这时每个魔方的售价为28元．
    （1）求魔方的进价？
    （2）超市卖出一半后，正好赶上双十一促销，商店决定将剩下的魔方以每3个80元的价格出售，很快销售一空，这批魔方超市共获利2800元，求该超市共购进四阶魔方多少个？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】平行四边形ABCD中，对角线AC、BD相交于点O，BD=2AD，E、F、G分别是OC、OD，AB的中点．下列结论：①EG=EF； ②△EFG≌△GBE； ③FB平分∠EFG；④EA平分∠GEF；⑤四边形BEFG是菱形．
    其中正确的是.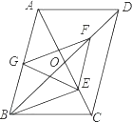

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果一个角的度数为31°42′，那么它的补角的度数为°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若x=﹣1是方程2x+a=0的解，则a=_____．

    查看答案和解析>>

    同步练习册答案