
分析 本题可利用一元二次方程的知识,设一条对角线为2a,另外一条为2b.面积S=$\frac{1}{2}$×2a×2b=2ab,再根据两条对角线之和为1,即a+b=$\frac{1}{2}$,设边长是m,则m2=a2+b2,根据a2+b2=(a+b)2-2ab,即可求得边长.
解答 解:设边长为m,一条对角线为2a,另外一条为2b,则
a+b=$\frac{1}{2}$,2ab=S,
∵m2=a2+b2=(a+b)2-2ab=$\frac{1}{4}$-S
∴m=$\frac{1}{2}$$\sqrt{1-4S}$,
故答案为:$\frac{1}{2}$$\sqrt{1-4S}$.
点评 此题主要考查菱形的性质和一元二次方程的应用,有难度,注意:菱形的对角线互相平分,菱形的四条边都相等.


 全能练考卷系列答案
全能练考卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2017届江苏省无锡市九年级下学期第一次模拟考试数学试卷(解析版) 题型:单选题
现有A、B两枚均匀的小立方体(立方体的每个面上分别标有数字1,2,3,4,5,6).用小莉掷A立方体朝上的数字为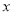 、小明掷B立方体朝上的数字为
、小明掷B立方体朝上的数字为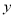 来确定点P(
来确定点P(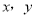 ),那么它们各掷一次所确定的点P落在已知抛物线
),那么它们各掷一次所确定的点P落在已知抛物线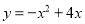 上的概率为( )
上的概率为( )
A. 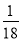 B.
B. 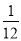 C.
C. 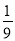 D.
D. 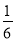
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com