
【题目】如图,将△ABC 分别沿 AB,AC 翻折得到△ABD 和△AEC,线段 BD 与AE 交于点 F.
(1)若∠ABC=16,∠ACB=30°,求∠DAE 及∠BFE 的值;
(2)若 BD 与 CE 所在的直线互相垂直,求∠CAB 的度数.
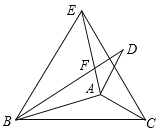
【答案】(1)42°,108°;(2)135°.
【解析】
由“∠ABC=16,∠ACB=30°”可以求出∠BAC的度数,根据翻折的性质可以求出∠DAE与∠BFE的度数,由“BD 与 CE 所在的直线互相垂直”可得∠DBC+∠ECB=90°,再利用翻折的性质可求出答案
解:(1)∵∠ABC=16°,∠ACB=30°,
∴∠BAC=134°,
∵△ABC≌△ABD,△ABC≌△AEC,
∴∠BAD=∠EAC=134°;∠DAE=134°×3-360°=42°.
∵∠D=∠ACB=30°,
∴∠BFE=∠DFA=180°-42°-30°=108°;
(2)∵BD 所在直线与 CE 所在直线互相垂直,
∴∠DBC+∠ECB=90°,
∵翻折
∴∠ABC=![]() ∠DBC ∠ACB =
∠DBC ∠ACB =![]() ∠ECB
∠ECB
∴∠ABC+∠ACB= ![]() ( ∠DBC+∠ECB )=45°,
( ∠DBC+∠ECB )=45°,
∴∠CAB=180°-(∠ABC+∠ACB )= 135°.


科目:初中数学 来源: 题型:
【题目】如图,AB是一垂直于水平面的建筑物,某同学从建筑物底端B出发,先沿水平方向向右行走20米到达点C,再经过一段坡度(或坡比)为i=1:0.75、坡长为10米的斜坡CD到达点D,然后再沿水平方向向右行走40米到达点E(A,B,C,D,E均在同一平面内).在E处测得建筑物顶端A的仰角为24°,则建筑物AB的高度约为(参考数据:sin24°≈0.41,cos24°≈0.91,tan24°=0.45)( )

A. 21.7米 B. 22.4米 C. 27.4米 D. 28.8米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点P是直角三角形ABC斜边AB上一动点(不与A,B重合),分别过A,B向直线CP作垂线,垂足分别为E,F,Q为斜边AB的中点。
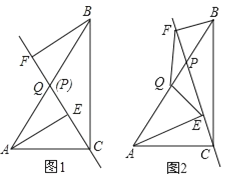
(1)如图1,当点P与点Q重合时,AE与BF的位置关系是___,QE与QF的数量关系是___;
(2)如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠α的顶点在正n边形的中心点O处,∠α绕着顶点O旋转,角的两边与正n边 形的两边分别交于点M、N,∠α与正n边形重叠部分面积为S.
(1)当n=4,边长为2,∠α=90°时,如图(1),请直接写出S的值;

(2)当n=5,∠α=72°时,如图(2),请问在旋转过程中,S是否发生变化?并说明理由;

(3)当n=6,∠α=120°时,如图(3),请猜想S是原正六边形面积的几分之几(不必说明理由).若∠α的平分线与BC边交于点P,判断四边形OMPN的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两小朋友都从![]() 地出发,匀速步行到
地出发,匀速步行到![]() 地(
地(![]() 、
、![]() 两地之间为笔直的道路)甲出发半分钟后,乙才从
两地之间为笔直的道路)甲出发半分钟后,乙才从![]() 地出发,经过一段时间追上甲,两人继续向
地出发,经过一段时间追上甲,两人继续向![]() 地步行,当甲、乙之间的距离刚好是70米时,乙立刻掉头以原速度向
地步行,当甲、乙之间的距离刚好是70米时,乙立刻掉头以原速度向![]() 地步行,半分钟后与甲相遇,乙又立刻掉头向
地步行,半分钟后与甲相遇,乙又立刻掉头向![]() 地以原速度步行(两次掉头时间忽略不计).甲、乙相距的路程为
地以原速度步行(两次掉头时间忽略不计).甲、乙相距的路程为![]() (米)与乙出发的时
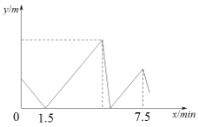
(米)与乙出发的时![]() (分钟)之间的关系如图所示,当乙到达
(分钟)之间的关系如图所示,当乙到达![]() 地时,甲与
地时,甲与![]() 地相距的路程是__________米.
地相距的路程是__________米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC.
(1)如图(1),∠C>∠B,若 AD⊥BC 于点 D,AE 平分∠BAC,你能找出∠EAD 与∠B,∠C 之间的数量关系吗?并说明理由.
(2)如图(2),AE 平分∠BAC,F 为 AE 上一点,FM⊥BC 于点 M,∠EFM 与∠B,∠C之间有何数量关系?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB∥CD,AD∥BC, AB=3,BC=4,将矩形纸片沿BD折叠,使点A落在点E处,设DE与BC相交于点F.
(1)判断△BDF的形状,并说明理由;
(2)求DF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A.关于某直线对称的两个三角形是全等三角形B.全等三角形是关于某直线对称的
C.两个图形关于某直线对称,则这两个图形一定分别位于这条直线的两侧D.有一条公共边的两个全等三角形关于公共边所在的直线对称
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,以AB为直径的⊙O分别与BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为5,∠CDF=30°,求![]() 的长(结果保留π).
的长(结果保留π).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com