
【题目】已知,点P是直角三角形ABC斜边AB上一动点(不与A,B重合),分别过A,B向直线CP作垂线,垂足分别为E,F,Q为斜边AB的中点。
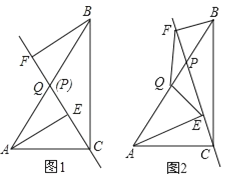
(1)如图1,当点P与点Q重合时,AE与BF的位置关系是___,QE与QF的数量关系是___;
(2)如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;
【答案】(1)AE∥BF,QE=QF (2)答案见解析
【解析】
(1)根据AAS推出△AEQ≌△BFQ,推出AE=BF即可;
(2)延长EQ交BF于D,求出△AEQ≌△BDQ,根据全等三角形的性质得出EQ=QD,根据直角三角形斜边上中点性质得出即可.
(1)AE∥BF,QE=QF,
理由是:如图1,∵Q为AB中点,

∴AQ=BQ,
∵BF⊥CP,AE⊥CP,
∴BF∥AE,∠BFQ=∠AEQ=90,
在△BFQ和△AEQ中

∴△BFQ≌△AEQ(AAS),
∴QE=QF,
故答案为:AE∥BF;QE=QF.
(2)QE=QF,
证明:如图2,延长FQ交AE于D,

∵Q为AB中点,
∴AQ=BQ,
∵BF⊥CP,AE⊥CP,
∴BF∥AE,
∴∠QAD=∠FBQ,
在△FBQ和△DAQ中

∴△FBQ≌△DAQ(ASA),
∴QF=QD,
∵AE⊥CP,
∴EQ是直角三角形DEF斜边上的中线,
∴QE=QF=QD,
即QE=QF.


 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:
【题目】四边形ABCD中,∠A=140°,∠D=80°.

(1)如图1,若∠B=∠C,试求出∠C的度数;
(2)如图2,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
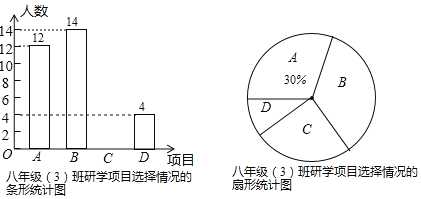
【题目】某学校开展以素质提升为主题的研学活动,推出了以下四个项目供学生选择:A.模拟驾驶;B.军事竞技;C.家乡导游;D.植物识别.学校规定:每个学生都必须报名且只能选择其中一个项目.八年级(3)班班主任刘老师对全班学生选择的项目情况进行了统计,并绘制了如下两幅不完整的统计图.请结合统计图中的信息,解决下列问题:
(1)八年级(3)班学生总人数是 ,并将条形统计图补充完整;
(2)刘老师发现报名参加“植物识别”的学生中恰好有两名男生,现准备从这些学生中任意挑选两名担任活动记录员,请用列表或画树状图的方法,求恰好选中1名男生和1名女生担任活动记录员的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC和△BDE都是等边三角形。则下列结论:①AE=CD.②BF=BG.③HB⊥FG.④∠AHC=60.⑤△BFG是等边三角形,其中正确的有___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机小李某天上午营运时是在东西走向的大街上进行的,如果规定向东为正,向西为负,他这天上午所接六位乘客的行车里程(单位:![]() )如下:
)如下:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
问:(1)将最后一位乘客送到目的地时,小李在什么位置?
(2)若汽车耗油量为![]() (升/千米),这天上午小李接送乘客,出租车共耗油多少升?
(升/千米),这天上午小李接送乘客,出租车共耗油多少升?
(3)若出租车起步价为8元,起步里程为![]() (包括
(包括![]() ),超过部分每千米1.2元,问小李这天上午共得车费多少元?
),超过部分每千米1.2元,问小李这天上午共得车费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() x2﹣
x2﹣![]() x+
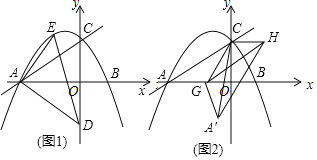
x+![]() 与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.
与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.
(1)求该抛物线的对称轴和线段AB的长;
(2)如图1,已知点D(0,﹣![]() ),点E是直线AC上访抛物线上的一动点,求△AED的面积的最大值;
),点E是直线AC上访抛物线上的一动点,求△AED的面积的最大值;
(3)如图2,点G是线段AB上的一动点,点H在第一象限,AC∥GH,AC=GH,△ACG与△A′CG关于直线CG对称,是否存在点G,使得△A′CH是直角三角形?若存在,请直接写出点G的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我省某工艺厂为全运会设计了一款成本为每件20元得工艺品,投放市场进行试销后发现每天的销售量y(件)是售价x(元∕件)的一次函数,当售价为22元∕件时,每天销售量为780件;当售价为25元∕件时,每天的销售量为750件.
(1)求y与x的函数关系式;
(2)如果该工艺品售价最高不能超过每件30元,那么售价定为每件多少元时,工艺厂销售该工艺品每天获得的利润最大?最大利润是多少元?(利润=售价﹣成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
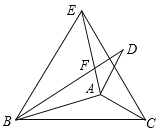
【题目】如图,将△ABC 分别沿 AB,AC 翻折得到△ABD 和△AEC,线段 BD 与AE 交于点 F.
(1)若∠ABC=16,∠ACB=30°,求∠DAE 及∠BFE 的值;
(2)若 BD 与 CE 所在的直线互相垂直,求∠CAB 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x(x-2)=x-2①与一元一次方程2x+1=2a-x②.
(1)若方程①的一个根是方程②的根,求a的值;
(2)若方程②的根不小于方程①两根中的较小根且不大于方程①两根中的较大根,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com