
【题目】如图,抛物线y=﹣![]() x2﹣
x2﹣![]() x+
x+![]() 与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.
与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.
(1)求该抛物线的对称轴和线段AB的长;
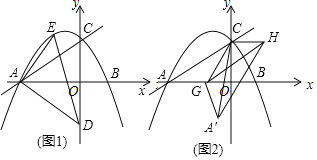
(2)如图1,已知点D(0,﹣![]() ),点E是直线AC上访抛物线上的一动点,求△AED的面积的最大值;
),点E是直线AC上访抛物线上的一动点,求△AED的面积的最大值;
(3)如图2,点G是线段AB上的一动点,点H在第一象限,AC∥GH,AC=GH,△ACG与△A′CG关于直线CG对称,是否存在点G,使得△A′CH是直角三角形?若存在,请直接写出点G的坐标;若不存在,请说明理由.
【答案】(1)AB=4,抛物线的对称轴x=﹣1;(2)m=﹣![]() 时,S△AED有最大值,最大值为
时,S△AED有最大值,最大值为![]() ;(3)满足条件点G坐标为(﹣1,0)或(0,0)或(1,0).
;(3)满足条件点G坐标为(﹣1,0)或(0,0)或(1,0).
【解析】
(1)利用待定系数法即可解决问题;
(2)如图1中,设E(m,﹣![]() m2﹣
m2﹣![]() m+
m+![]() ),根据S△AED=S△AOD+S△AEO+S△ECO-S△ECD根据二次函数,利用二次函数的性质即可解决问题;
),根据S△AED=S△AOD+S△AEO+S△ECO-S△ECD根据二次函数,利用二次函数的性质即可解决问题;
(3)分三种情形①如图2中,连接BC.当点A′在y轴上时,∠HCA′=90°满足条件.②如图3中,当点G与点O重合时,易证四边形GCHA′是矩形,此时△CHA′是直角三角形;③如图4中,当点G与B重合时,四边形GCHA′是矩形,此时△CHA′是直角三角形.
解:(1)对于y=﹣![]() x2﹣
x2﹣![]() x+
x+![]() 令y=0,可得﹣
令y=0,可得﹣![]() x2﹣
x2﹣![]() x+
x+![]() =0,
=0,
解得x=﹣3或1,
∴A(﹣3,0),B(1,0),
∴AB=4,
抛物线的对称轴x=﹣![]() =﹣
=﹣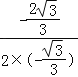 =﹣1.
=﹣1.
(2)如图1中,设E(m,﹣![]() m2﹣
m2﹣![]() m+
m+![]() ),
),
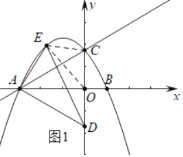
∵S△AED=S△AOD+S△AEO+S△ECO﹣S△ECD
=![]() ×3×
×3×![]() +
+![]() ×3×(﹣
×3×(﹣![]() m2﹣
m2﹣![]() m+
m+![]() )+
)+![]() ×
×![]() ×(﹣m)﹣
×(﹣m)﹣![]() ×2
×2![]() ×(﹣m)
×(﹣m)
=﹣![]() (m+
(m+![]() )2+
)2+![]() ,
,
∵﹣![]() <0,
<0,
∴m=﹣![]() 时,S△AED有最大值,最大值为
时,S△AED有最大值,最大值为![]() .
.
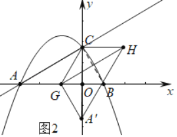
(3)①如图2中,连接BC.
∵AC∥GH,AC=GH,
∴四边形ACHG是平行四边形,
∴CH∥AB,
当点A′在y轴上时,∠HCA′=90°满足条件.
∵AO=3,OC=![]() ,OB=1,
,OB=1,
∴tan∠CAO=![]() =
=![]() ,tan∠BCO=
,tan∠BCO=![]() =
=![]() ,
,
∴∠CAO=30°,∠OCB=30°,
∴∠ACO=60°,
∴∠ACB=∠ACO+∠OCB=90°,
当点A′在y轴上时,∠ACG=∠A′CG=30°,
∴OG=OCtan30°=1,
∴G(﹣1,0).
②如图3中,当点G与点O重合时,易证四边形GCHA′是矩形,此时△CHA′是直角三角形;
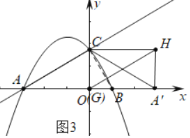
③如图4中,当点G与B重合时,四边形GCHA′是矩形,此时△CHA′是直角三角形,G(1,0),
综上所述,满足条件点G坐标为(﹣1,0)或(0,0)或(1,0).


科目:初中数学 来源: 题型:
【题目】如图,已知EF//AD, ∠1=∠2, ∠BAC=70°.求∠AGD的度数(将以下过程填写完整)

解:∵EF//AD
∴∠2=
又∵∠1=∠2
∴∠1=∠3
∴ AB//
∴∠BAC+ =180°.
又∵∠BAC=70°
∴∠AGD= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一列数:1,―2,3,―4,5,―6,7,… 将这列数排成下列形式:
第1行 1
第2行 -2 3
第3行 -4 5 -6
第4行 7 -8 9 -10
第5行 11 -12 13 -14 15
… …
按照上述规律排下去,那么第10行从左边数第5个数等于
A.50B.-50C.60D.-60
查看答案和解析>>
科目:初中数学 来源: 题型:
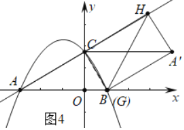
【题目】已知,点P是直角三角形ABC斜边AB上一动点(不与A,B重合),分别过A,B向直线CP作垂线,垂足分别为E,F,Q为斜边AB的中点。
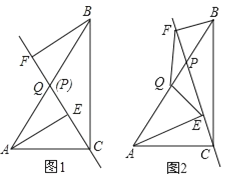
(1)如图1,当点P与点Q重合时,AE与BF的位置关系是___,QE与QF的数量关系是___;
(2)如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠α的顶点在正n边形的中心点O处,∠α绕着顶点O旋转,角的两边与正n边 形的两边分别交于点M、N,∠α与正n边形重叠部分面积为S.
(1)当n=4,边长为2,∠α=90°时,如图(1),请直接写出S的值;

(2)当n=5,∠α=72°时,如图(2),请问在旋转过程中,S是否发生变化?并说明理由;

(3)当n=6,∠α=120°时,如图(3),请猜想S是原正六边形面积的几分之几(不必说明理由).若∠α的平分线与BC边交于点P,判断四边形OMPN的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC.
(1)如图(1),∠C>∠B,若 AD⊥BC 于点 D,AE 平分∠BAC,你能找出∠EAD 与∠B,∠C 之间的数量关系吗?并说明理由.
(2)如图(2),AE 平分∠BAC,F 为 AE 上一点,FM⊥BC 于点 M,∠EFM 与∠B,∠C之间有何数量关系?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
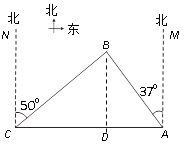
【题目】南中国海是中国固有领海,我渔政船经常在此海域执勤巡察.一天我渔政船停在小岛A北偏西37°方向的B处,观察A岛周边海域.据测算,渔政船距A岛的距离AB长为10海里.此时位于A岛正西方向C处的我渔船遭到某国军舰的袭扰,船长发现在其北偏东50°的方向上有我方渔政船,便发出紧急求救信号.渔政船接警后,立即沿BC航线以每小时30海里的速度前往救助,问渔政船大约需多少分钟能到达渔船所在的C处?
![]() (参考数据:sin37°≈0.60,cos37°≈0.80,sin50°≈0.77,cos50°≈0.64,sin53°≈0.80,cos53°≈0.60,sin40°≈0.64,cos40°≈0.77)
(参考数据:sin37°≈0.60,cos37°≈0.80,sin50°≈0.77,cos50°≈0.64,sin53°≈0.80,cos53°≈0.60,sin40°≈0.64,cos40°≈0.77)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com