
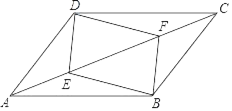
【题目】已知:如图,E、F是ABCD的对角线AC上的两点,AF=CE.
求证:(1)△ABE≌△CDF;
(2)ED∥BF.
【答案】(1)见解析;(2)见解析
【解析】
(1)根据已知条件得到AE=CF,根据平行四边形的性质得到∠DCF=∠BAE,根据全等三角形的判定定理即可得到结论;
(2)根据全等三角形的性质得到BE=DF,∠AEB=∠CFD,根据平行四边形的判定和性质即可得到结论.
证明:(1)∵AF=CE,
∴AF﹣EF=CE﹣EF,
即AE=CF,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠DCF=∠BAE,
在△ABE与△CDF中,
∵![]() ,
,
![]() ,
,
![]() ,
,
∴△ABE≌△CDF(SAS);
(2)∵△ABE≌△CDF,
∴BE=DF,∠AEB=∠CFD,
∴∠BEF=∠DFE,
∴BE∥DF,
∴四边形DEBF是平行四边形,
∴ED∥BF.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:
【题目】若一个四位自然数n满足千位与个位相同,百位与十位相同,我们称这个数为“天平数”.将“天平数”n的前两位与后两位交换位置得到一个新的“天平数”n′,记F(n)=![]() ,例如n=2112,n′=1221,F(2112)=
,例如n=2112,n′=1221,F(2112)=![]() =9
=9
(1)计算F(5335)= ;若“天平数”n满足F(n)是一个完全平方数,求F(n)的值;
(2)s、t“天平数“,其中s=![]() ,t=
,t=![]() (1≤b<a≤9,1≤x<y≤9且a,b, xy为整数),若F(s)能被8整除,且F(s)+F(t)﹣9(y+1)=0,规定:K(s,t)=
(1≤b<a≤9,1≤x<y≤9且a,b, xy为整数),若F(s)能被8整除,且F(s)+F(t)﹣9(y+1)=0,规定:K(s,t)=![]() ,求K(s,t)的所有结果的值.
,求K(s,t)的所有结果的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
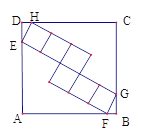
【题目】如图,正方形ABCD中,内部有6个全等的正方形,小正方形的顶点E、F、G、H分别在边AD、AB、BC、CD上,则tan∠DEH=( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边△ABC,点D在直线BC上,连接AD,作∠ADN=60°,直线DN交射线AB于点E,过点C作CF∥AB交直线DN于点F.
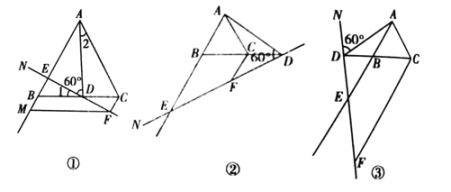
(1)当点D在线段BC上,∠NDB为锐角时,如图①.
①判断∠1与∠2的大小关系,并说明理由;
②过点F作FM∥BC交射线AB于点M,求证:CF+BE=CD;
(2)①当点D在线段BC的延长线上,∠NDB为锐角时,如图②,请直接写出线段CF,BE,CD之间的数量关系;
②当点D在线段CB的延长线上,∠NDB为钝角或直角时,如图③,请直接写出线段CF,BE,CD之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:法国数学家韦达在研究一元二次方程时有一项重大发现:如果一元二次方程![]() 的两个根分别是
的两个根分别是![]() ,那么
,那么![]() ,
,![]() .
.
例如:已知方程![]() 的两根分别是
的两根分别是![]() ,
,
则:![]() ,
,![]() .
.
请同学们阅读后利用以上结论完成以下问题:
(1)已知方程![]() 的两根分别是
的两根分别是![]() ,求
,求![]() 和
和![]() 的值;
的值;
(2)已知方程![]() 的两根分别是
的两根分别是![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(3)若一元二次方程![]() 的一个根大于2,一个根小于2,求
的一个根大于2,一个根小于2,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
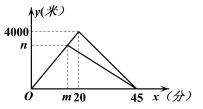
【题目】晓琳和爸爸到太子河公园运动,两人同时从家出发,沿相同路线前行,途中爸爸有事返回,晓琳继续前行5分钟后也原路返回,两人恰好同时到家.晓琳和爸爸在整个运动过程中离家的路程y1(米),y2(米)与运动时间x(分)之间的函数关系如图所示,下列结论:①两人同行过程中的速度为200米/分;②m的值是15,n的值是3000;③晓琳开始返回时与爸爸相距1800米;④运动18分钟或30分钟时,两人相距900米.其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,两个完全相同的三角形纸片![]() 和
和![]() 重合放置,其中
重合放置,其中![]() ,
,![]() .
.
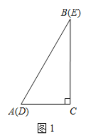
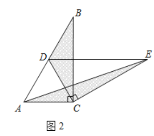

(1)操作发现:如图2,固定![]() ,使
,使![]() 绕点
绕点![]() 旋转,当点
旋转,当点![]() 恰好落在
恰好落在![]() 边上时,填空:①线段
边上时,填空:①线段![]() 与
与![]() 的位置关系是________;②设
的位置关系是________;②设![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,则
,则![]() 与
与![]() 的数量关系是_____.
的数量关系是_____.
(2)猜想论证:当![]() 绕点
绕点![]() 旋转到如图3所示的位置时,请猜想(1)中
旋转到如图3所示的位置时,请猜想(1)中![]() 与
与![]() 的数量关系是否仍然成立?若成立,请证明;若不成立,请说明理由.
的数量关系是否仍然成立?若成立,请证明;若不成立,请说明理由.
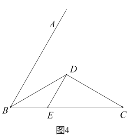
(3)拓展探究:已知![]() ,
,![]() 平分
平分![]() ,
,![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() (如图4).若在射线
(如图4).若在射线![]() 上存在点
上存在点![]() ,使
,使![]() ,请求相应的
,请求相应的![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com