
【题目】若一个四位自然数n满足千位与个位相同,百位与十位相同,我们称这个数为“天平数”.将“天平数”n的前两位与后两位交换位置得到一个新的“天平数”n′,记F(n)=![]() ,例如n=2112,n′=1221,F(2112)=
,例如n=2112,n′=1221,F(2112)=![]() =9
=9
(1)计算F(5335)= ;若“天平数”n满足F(n)是一个完全平方数,求F(n)的值;
(2)s、t“天平数“,其中s=![]() ,t=
,t=![]() (1≤b<a≤9,1≤x<y≤9且a,b, xy为整数),若F(s)能被8整除,且F(s)+F(t)﹣9(y+1)=0,规定:K(s,t)=
(1≤b<a≤9,1≤x<y≤9且a,b, xy为整数),若F(s)能被8整除,且F(s)+F(t)﹣9(y+1)=0,规定:K(s,t)=![]() ,求K(s,t)的所有结果的值.
,求K(s,t)的所有结果的值.
【答案】(1)18,F(n)=0或9或36;(2)![]() 或
或![]() 或
或![]() .
.
【解析】
(1)根据天平数的定义即可解答.
(2)根据(1)的方法分别求出a,b,x,y的值即可进行解答.
解:(1)根据“天平数”的意义得,5335的“天平数”为3553,
∴F(5335)=![]() =18,
=18,
故答案为:18,
设n为![]() ,(0<c≤9,0<d≤9),则它的“天平数”n'为
,(0<c≤9,0<d≤9),则它的“天平数”n'为![]() ,
,
∴n=1000c+100d+10d+c=1001c+110d,
n'=1000d+100c+10c+d=1001d+110c,
∴n﹣n'=1001c+110d﹣(1001d+110c)=891(c﹣d),
∴F(n)=![]() =
=![]() =9(c﹣d),
=9(c﹣d),
∵F(n)是一个完全平方数,
∴(c﹣d)是一个完全平方数,
∵0<c≤9,0<d≤9,
∴0≤c﹣d<9,
∴c﹣d=0或1或4,
∴F(n)=0或9或36;
(2)同(1)的方法得,F(s)=9(a﹣b),0≤a﹣b≤9,
∵F(s)能被8整除,
∴a﹣b=8,
∴F(s)=72,a=b+8,
同(1)的方法得,F(t)=9(x﹣y),
∵F(s)+F(t)﹣9(y+1)=0,
∴72+9(x﹣y)﹣9(y+1)=0,
∴x=2y﹣7,
∵1≤x<y≤9,
∴x=1,y=4或x=3,y=5或x=5,y=6,
∴K(s,t)=![]() =
=![]() =
=![]() =
=![]() =
=![]() =
=![]() 或
或![]() 或
或![]() .
.


 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
【题目】某中学积极组织学生开展课外阅读活动,为了解本校学生每周课外阅读的时间量t(单位:小时),采用随机抽样的方法抽取部分学生进行了问卷调查,调查结果按0≤t<2,2≤t<3,3≤t<4,t≥4分为四个等级,并分别用A、B、C、D表示,根据调查结果统计数据绘制成了如图所示的两幅不完整的统计图,由图中给出的信息解答下列问题:

(1)求出x的值,并将不完整的条形统计图补充完整;
(2)若该校共有学生2500人,试估计每周课外阅读时间量满足2≤t<4的人数;
(3)若本次调查活动中,九年级(1)班的两个学习小组分别有3人和2人每周阅读时间量都在4小时以上,现从这5人中任选2人参加学校组织的知识抢答赛,求选出的2人来自不同小组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是正
是正![]() 内一点,
内一点,![]() ,
,![]() ,
,![]() ,将线段
,将线段![]() 以点
以点![]() 为旋转中心逆时针旋转60°得到线段
为旋转中心逆时针旋转60°得到线段![]() ,连接
,连接![]() ,下列结论:①
,下列结论:①![]() 可以由
可以由![]() 绕点
绕点![]() 逆时针旋转60°得到:②点
逆时针旋转60°得到:②点![]() 与
与![]() 的距离为4;③
的距离为4;③![]() ;④
;④![]() 四边形
四边形![]() ;⑤
;⑤![]() .其中正确的结论是( )
.其中正确的结论是( )
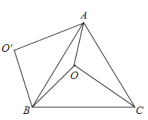
A.①②③④B.①②③⑤C.①②④⑤D.①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,平行四边形ABCD在第一象限,且AB∥x轴.直线y=-x从原点出发沿x轴正方向平移,在平移过程中直线被平行四边形截得的线段长度l与直线在x轴上平移的距离m的函数图象如图②,那么平行四边形ABCD的面积为()
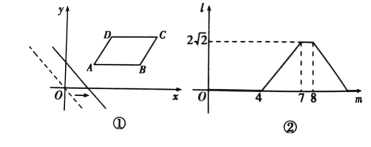
A.4B.![]() C.
C.![]() D.8
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 是等腰直角三角形,动点
是等腰直角三角形,动点![]() 在斜边
在斜边![]() 所在的直线上,以
所在的直线上,以![]() 为直角边作等腰直角三角形
为直角边作等腰直角三角形![]() ,其中
,其中![]() ,探究并解决下列问题:
,探究并解决下列问题:
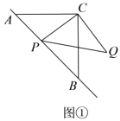
(1)如图①,若点![]() 在线段
在线段![]() 上,且
上,且![]() ,
,![]() ,则:
,则:
①![]() 长为
长为![]() ;
;![]() 的长为 ;
的长为 ;
②猜想:![]() ,
,![]() ,
,![]() 三者之间的数量关系为 ;
三者之间的数量关系为 ;
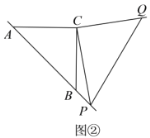
(2)如图②,若点![]() 在
在![]() 的延长线上,在(1)中所猜想的结论依然成立,请你利用图②给出证明过程;
的延长线上,在(1)中所猜想的结论依然成立,请你利用图②给出证明过程;
(3)若动点![]() 满足
满足![]() ,求
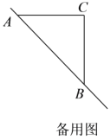
,求![]() 的值.(提示:请利用备用图进行探求)
的值.(提示:请利用备用图进行探求)
查看答案和解析>>
科目:初中数学 来源: 题型:
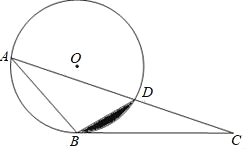
【题目】如图,△ABC中,⊙O经过A、B两点,且交AC于点D,连接BD,∠DBC=∠BAC.
(1)证明BC与⊙O相切;
(2)若⊙O的半径为6,∠BAC=30°,求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com