
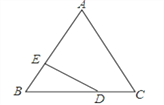
【题目】如图,D为等边△ABC边BC上一点,DE⊥AB于E,若BD:CD=2:1,DE=2![]() , 求AE.
, 求AE.
【答案】4
【解析】试题分析:由等边三角的性质可得:AB=BC,∠B=60°,由DE⊥AB于E,可得:∠DEB=90°,∠BDE=30°,由直角三角形中30°角所对的直角边等于斜边的一半,可得:BD=2BE,然后由勾股定理可求BE和BD的值,再由BD:CD=2:1,可求CD的长,进而确定BC的长,由AB=BC即可求出AE的长.
试题解析:∵△ABC是等边三角形,
∴AB=BC,∠B=60°,
∵DE⊥AB于E,
∴∠DEB=90°,
∴∠BDE=30°,
∴BD=2BE,
在Rt△BDE中,设BE=x,则BD=2x,
∵DE=2![]() ,
,
由勾股定理得:(2x)2﹣x2=(2![]() )2 ,
)2 ,
解得:x=2,
所以BE=2,BD=4,
∵BD:CD=2:1,
∴CD=2,
∴BC=BD+CD=6,
∵AB=BC,
∴AB=6,
∵AE=AB﹣BE
∴AE=6﹣2=4.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】小明解方程![]() =3出现了错误,解答过程如下:
=3出现了错误,解答过程如下:
方程两边都乘以(x-2),得1-(1-x)=3(第一步)
去括号,得1-1+x=3(第二步)
移项,合并同类项,得x=3(第三步)
检验,当x=3时x-2≠0(第四步)
所以x=3是原方程的解.(第五步)
(1)小明解答过程是从第____步开始出错的,原方程化为第一步的根据是_____.
(2)请写出此题正确的解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,弹性小球从P(2,0)出发,沿所示方向运动,每当小球碰到正方形OABC的边时反弹,反弹时反射角等于入射角,当小球第一次碰到正方形的边时的点为P1,第二次碰到正方形的边时的点为P2…,第n次碰到正方形的边时的点为Pn,则P2020的坐标是( )
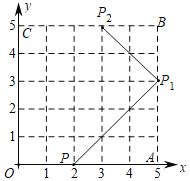
A.(5,3)B.(3,5)C.(0,2)D.(2,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:将边长为![]() 的正三角形的三条边分别
的正三角形的三条边分别![]() 等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
探究:要研究上面的问题,我们不妨先从最简单的情形入手,进而找到一般性规律.
探究一:将边长为2的正三角形的三条边分别二等分,连接各边中点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
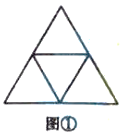
如图①,连接边长为2的正三角形三条边的中点,从上往下看:
边长为1的正三角形,第一层有1个,第二层有3个,共有![]() 个;
个;
边长为2的正三角形一共有1个.
探究二:将边长为3的正三角形的三条边分别三等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
如图②,连接边长为3的正三角形三条边的对应三等分点,从上往下看:边长为1的正三角形,第一层有1个,第二层有3个,第三层有5个,共有![]() 个;边长为2的正三角形共有
个;边长为2的正三角形共有![]() 个.
个.

探究三:将边长为4的正三角形的三条边分别四等分(图③),连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
(仿照上述方法,写出探究过程)

结论:将边长为![]() 的正三角形的三条边分别
的正三角形的三条边分别![]() 等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
(仿照上述方法,写出探究过程)
应用:将一个边长为25的正三角形的三条边分别25等分,连接各边对应的等分点,则该三角形中边长为1的正三角形有______个和边长为2的正三角形有______个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节前小明花1200元从市场购进批发价分别为每箱30元与50元的![]() 、
、![]() 两种水果进行销售,分别以每箱35元与60元的价格出售,设购进
两种水果进行销售,分别以每箱35元与60元的价格出售,设购进![]() 水果
水果![]() 箱,
箱,![]() 水果
水果![]() 箱.
箱.
(1)求![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)若要求购进![]() 水果的数量不少于
水果的数量不少于![]() 水果的数量,则应该如何分配购进
水果的数量,则应该如何分配购进![]() 、
、![]() 水果的数量并全部售出才能获得最大利润,此时最大利润是多少?
水果的数量并全部售出才能获得最大利润,此时最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《代数学》中记载,形如x2+8x=33的方程,求正数解的几何方法是:“如图1,先构造一个面积为x2的正方形,再以正方形的边长为一边向外构造四个面积为2x的矩形,得到大正方形的面积为33+16=49,则该方程的正数解为7﹣4=3.”小聪按此方法解关于x的方程x2+10x+m=0时,构造出如图2所示的图形,已知阴影部分的面积为50,则该方程的正数解为( )


A.6B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】开学初,李芳和王平去文具店购买学习用品,李芳用18元钱买了1支钢笔和3本笔记本;王平用30元买了同样的钢笔2支和笔记本4本.
(1)求每支钢笔和每本笔记本的价格;
(2)校运会后,班主任拿出200元学校奖励基金交给班长,购买上述价格的钢笔笔记本共36件作为奖品,奖给校运会中表现突出的同学,要求笔记本数不多于钢笔数的2倍,共有多少种购买方案?请你一一写出.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图的方格中,每个小正方形的边长都为1,△ABC的顶点均在格点上.在建立平面直角坐标系后,点B的坐标为(﹣1,2).
(1)把△ABC向下平移8个单位后得到对应的△A1B1C1,画出△A1B1C1,并写出A1坐标是 .
(2)以原点O为对称中心,画出与△ABC关于原点O对称的△A2B2C2,并写出B2坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了让学生能更加了解温州历史,某校组织七年级师生共480人参观温州博物馆.学校向租车公司租赁A、B两种车型接送师生往返,若租用A型车3辆,B型车6辆,则空余15个座位;若租用A型车5辆,B型车4辆,则15人没座位.
(1)求A、B两种车型各有多少个座位;
(2)若A型车日租金为350元,B型车日租金为400元,且租车公司最多能提供7辆B型车,应怎样租车能使座位恰好坐满且租金最少,并求出最少租金.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com