
【题目】已知,如图![]() ,且
,且![]() ,
,![]() .其中
.其中![]() 、
、![]() 、
、![]() 共线且
共线且![]() 交
交![]() 于
于![]() .
.
(1)如图1,若![]() 为
为![]() 的中点,且
的中点,且![]() ,求
,求![]() 的长.
的长.
(2)如图2,若![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,求证:
,求证:![]()

【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)只要证明△DAC≌△EAB,推出CD=EB,∠ACD=∠ABE,由∠CFD=∠AFB,推出∠CDF=∠FAB=90°,再求出CD、BD,利用勾股定理求出BC即可解决问题.
(2)如图2中,延长AE交BC于J.想办法证明CA=CJ,BJ=BG即可解决问题.
(1)如图1中,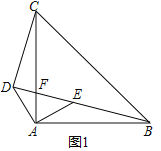
∵△ABC和△ADE均为等腰直角三角形,
∴∠BAC=∠EAD=90°,AB=AC,AE=AD=1,
∴∠EAB=∠DAC,
∴△DAC≌△EAB,
∴CD=EB=![]() ,∠ACD=∠ABE,
,∠ACD=∠ABE,
∵∠CFD=∠AFB,
∴∠CDF=∠FAB=90°,
∵DE=EB=CD=![]() ,
,
∴BC=![]() ,
,
∴AB=AC=![]() .
.
(2)如图2中,延长AE交BC于J.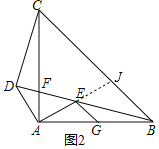
∵DE=![]() BE,DE=
BE,DE=![]() AE,
AE,
∴AE=EB,
∴∠EAB=∠EBA,
∵∠DEA=45°=∠EAB+∠EBA,
∵EF=BE,∠BAF=90°,
∴∠EAB=∠EBA=∠EBC=22.5°,
∴∠CAE=67.5°,
∴∠CJA=180°-∠CAJ-∠ACJ=67.5°,
∴∠CAJ=∠CJA,
∴CA=CJ=CB,
∵EG⊥AE,
∴∠AEG=∠GEJ=90°,
∴∠AGE=90°-22.5°=67.5°,
∵∠AGE=∠EBG+∠GEB,
∴∠BEG=45°=∠BEJ,
∵BE=BE,∠EBJ=∠EBG,
∴△EBJ≌△EBG(ASA),
∴BG=BJ,
∴BC=CJ+BJ=AB+BG.


 每课必练系列答案
每课必练系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若AB=![]() ,BD=2,求OE的长.
,BD=2,求OE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持AD=CE.连接DE、DF、EF.在此运动变化的过程中,下列结论:①△DFE是等腰直角三角形;②四边形CDFE不可能为正方形;③四边形CDFE的面积保持不变;④△CDE面积的最大值为8.其中正确的结论有( )个.
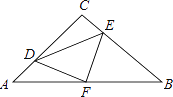
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是( )

A. 2 B. ![]() C.
C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学积极组织学生开展课外阅读活动,为了解本校学生每周课外阅读的时间量t(单位:小时),采用随机抽样的方法抽取部分学生进行了问卷调查,调查结果按0≤t<2,2≤t<3,3≤t<4,t≥4分为四个等级,并分别用A、B、C、D表示,根据调查结果统计数据绘制成了如图所示的两幅不完整的统计图,由图中给出的信息解答下列问题:

(1)求出x的值,并将不完整的条形统计图补充完整;
(2)若该校共有学生2500人,试估计每周课外阅读时间量满足2≤t<4的人数;
(3)若本次调查活动中,九年级(1)班的两个学习小组分别有3人和2人每周阅读时间量都在4小时以上,现从这5人中任选2人参加学校组织的知识抢答赛,求选出的2人来自不同小组的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com