
【题目】在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持AD=CE.连接DE、DF、EF.在此运动变化的过程中,下列结论:①△DFE是等腰直角三角形;②四边形CDFE不可能为正方形;③四边形CDFE的面积保持不变;④△CDE面积的最大值为8.其中正确的结论有( )个.
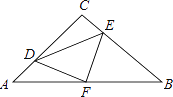
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】
连接CF,证明△ADF≌△CEF,根据全等三角形的性质判断①,根据正方形的判定定理判断②,根据全等三角形的性质判断③,求出△DEF的最小值判断④.
连接CF.
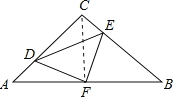 ∵△ABC为等腰直角三角形,
∵△ABC为等腰直角三角形,
∴∠FCB=∠A=45°,CF=AF=FB,
在△ADF和△CEF中,
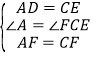 ,
,
∴△ADF≌△CEF,
∴EF=DF,∠CFE=∠AFD,
∵∠AFD+∠CFD=90°,
∴∠CFE+∠CFD=∠EFD=90°,
∴△EDF是等腰直角三角形,①正确;
当D. E分别为AC,BC的中点时,四边形CDEF是正方形,②错误;
∵△ADF≌△CEF,
∴![]() ,
,
∴四边形CDFE的面积![]() ,
,
∴四边形CDFE的面积保持不变,③正确;
∵△DEF是等腰直角三角形,
∴当DE最小时,DF也最小,
即当DF⊥AC时,DE最小,此时DF=![]() AC=4,
AC=4,
∴DE=![]() DF=
DF=![]() ,
,
当△CDE面积最大时,此时△DEF的面积最小,
∴![]() ,④正确,
,④正确,
故选:C.


科目:初中数学 来源: 题型:
【题目】一个长方形的周长是24厘米,它的一边长是![]() (单位:厘米),面积是
(单位:厘米),面积是![]() (单位:平方厘米).
(单位:平方厘米).
(1)若![]() ,则这个长方形的面积是__________平方厘米;
,则这个长方形的面积是__________平方厘米;
(2)写出![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)画出![]() 关于
关于![]() 的函数图象.
的函数图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,3×3的方格分为上中下三层,第一层有一枚黑色方块甲,可在方格A、B、C中移动,第二层有两枚固定不动的黑色方块,第三层有一枚黑色方块乙,可在方格D、E、F中移动,甲、乙移入方格后,四枚黑色方块构成各种拼图.

(1)若乙固定在E处,移动甲后黑色方块构成的拼图是轴对称图形的概率是________.
(2)若甲、乙均可在本层移动.
①用树形图或列表法求出黑色方块所构拼图是轴对称图形的概率________.
②黑色方块所构拼图是中心对称图形的概率是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 是等边三角形,作直线
是等边三角形,作直线![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,连接
,连接![]() ,直线
,直线![]() 交直线
交直线![]() 于点
于点![]() ,连接
,连接![]() .
.

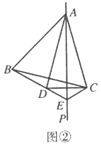

(1)如图①,求证:![]() ;(提示:在BE上截取
;(提示:在BE上截取![]() ,连接
,连接![]() .)
.)
(2)如图②、图③,请直接写出线段![]() ,
,![]() ,
,![]() 之间的数量关系,不需要证明;
之间的数量关系,不需要证明;
(3)在(1)、(2)的条件下,若![]() ,则
,则![]() __________.
__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某校九年级(3)班的一个学习小组进行测量小山高度的实践活动.部分同学在山脚A点处测得山腰上一点D的仰角为30°,并测得AD的长度为180米.另一部分同学在山顶B点处测得山脚A点的俯角为45°,山腰D点的俯角为60°,请你帮助他们计算出小山的高度BC.(计算过程和结果都不取近似值)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明准备测量一段水渠的深度,他把一根竹竿AB竖直插到水底,此时竹竿AB离岸边点C处的距离![]() 米。竹竿高出水面的部分AD长0.5米,如果把竹竿的顶端A拉向岸边点C处,竿顶和岸边的水面刚好相齐,则水渠的深度BD为( )
米。竹竿高出水面的部分AD长0.5米,如果把竹竿的顶端A拉向岸边点C处,竿顶和岸边的水面刚好相齐,则水渠的深度BD为( )

A. 2米B. 2.5米C. 2.25米D. 3米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,内部有6个全等的正方形,小正方形的顶点E、F、G、H分别在边AD、AB、BC、CD上,则tan∠DEH=( )
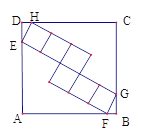
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com