
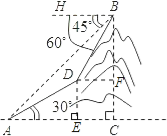
【题目】如图所示,某校九年级(3)班的一个学习小组进行测量小山高度的实践活动.部分同学在山脚A点处测得山腰上一点D的仰角为30°,并测得AD的长度为180米.另一部分同学在山顶B点处测得山脚A点的俯角为45°,山腰D点的俯角为60°,请你帮助他们计算出小山的高度BC.(计算过程和结果都不取近似值)

【答案】![]() 米
米
【解析】
试题首先根据题意分析图形;过点D作DE⊥AC于点E,作DF⊥BC于点F;构造本题涉及到的两个直角三角形,根据图形分别求解可得DE与BF的值,再利用BC=DE+BF,进而可求出答案.
解:如图,过点D作DE⊥AC于点E,作DF⊥BC于点F,
则有DE∥FC,DF∥EC.
∵∠DEC=90°,
∴四边形DECF是矩形,
∴DE=FC.
∵∠HBA=∠BAC=45°,
∴∠BAD=∠BAC﹣∠DAE=45°﹣30°=15度.
又∵∠ABD=∠HBD﹣∠HBA=60°﹣45°=15°,
∴△ADB是等腰三角形.∴AD=BD=180(米).
在Rt△AED中,sin∠DAE=sin30°=![]() ,
,
∴DE=180sin30°=180×![]() =90(米),∴FC=90米.
=90(米),∴FC=90米.
在Rt△BDF中,∠BDF=∠HBD=60°,sin∠BDF=sin60°=![]() ,
,
∴BF=180sin60°=180×![]() (米).
(米).
∴BC=BF+FC=90![]() +90=90(
+90=90(![]() +1)(米).
+1)(米).
答:小山的高度BC为90(![]() +1)米.
+1)米.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】
已知:如图(1),在平面直角坐标系中,点![]() ,
,![]() ,
,![]() 分别在坐标轴上,且
分别在坐标轴上,且![]() ,
,![]() 的面积为
的面积为![]() ,点
,点![]() 从
从![]() 点出发沿
点出发沿![]() 轴负方向以
轴负方向以![]() 个单位长度/秒的速度向下运动,连接
个单位长度/秒的速度向下运动,连接![]() ,
,![]() ,点
,点![]() 为
为![]() 上的中点.
上的中点.
(1)直接写出坐标![]() ___________,
___________,![]() ___________,
___________,![]() ___________.
___________.
(2)设点![]() 运动的时间为
运动的时间为![]() 秒,问:当
秒,问:当![]() 与
与![]() 垂直且相等时,求此时
垂直且相等时,求此时![]() 的值?并说明理由.
的值?并说明理由.
(3)如图(2)![]() ,在第四象限内有一动点
,在第四象限内有一动点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,点
,点![]() 在第四象限内运动,当
在第四象限内运动,当![]() ,判断
,判断![]() 是否平分
是否平分![]() ,并说明理由.
,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用适当的方法解下列方程
(1)x2﹣4x+1=0 (2)(5x﹣3)2+2(3﹣5x)=0
(3)(2x+1)2=(x﹣1)2 (4)4x2+2=7x.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() ,
,![]() 分别在
分别在![]() 轴,
轴,![]() 轴正半轴上.
轴正半轴上.



(1)![]() 的平分线与
的平分线与![]() 的外角平分线交于点
的外角平分线交于点![]() ,求
,求![]() 的度数;
的度数;
(2)设点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,且满足
,且满足![]() ,求
,求![]() 的面积;
的面积;
(3)在(2)的条件下,当![]() 是以
是以![]() 为斜边的等腰直角三角形时,请直接写出点
为斜边的等腰直角三角形时,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
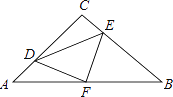
【题目】在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持AD=CE.连接DE、DF、EF.在此运动变化的过程中,下列结论:①△DFE是等腰直角三角形;②四边形CDFE不可能为正方形;③四边形CDFE的面积保持不变;④△CDE面积的最大值为8.其中正确的结论有( )个.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正比例函数y=kx的图象与反比例函数y=![]() (m≠0)的图象在第一象限交于点C,△ABC是边长为3的等边三角形,且AB边在x轴额正半轴上,cos∠COA=
(m≠0)的图象在第一象限交于点C,△ABC是边长为3的等边三角形,且AB边在x轴额正半轴上,cos∠COA=![]() .
.
(1)求k,m的值;
(2)点P在射线OC上,且OP=5![]() ,动点Q从点P出发先沿着适当的路径运动到线段AB中垂线上的点M处,再沿垂直于y轴的方向运动到y轴上的点N处,最后沿适当的路径运动到点A处停止,当点Q的运动路径最短时,求N点坐标及点Q运动的最短路程;
,动点Q从点P出发先沿着适当的路径运动到线段AB中垂线上的点M处,再沿垂直于y轴的方向运动到y轴上的点N处,最后沿适当的路径运动到点A处停止,当点Q的运动路径最短时,求N点坐标及点Q运动的最短路程;
(3)将△ABC绕点A进行旋转,在旋转过程中,设BC所在直线与射线OC相交于点R,与x轴正半轴交于点T,当△ORT为等腰三角形时,求OT的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com