
【题目】如图,菱形ABCD的边长为4,∠ABC=60°,在菱形ABCD内部有一点P,当PA+PB+PC值最小时,PB的长为________.

【答案】![]()
【解析】
将△APC绕点C顺时针旋转60°,得到△DEC,连接PE、DE,则线段BD即为PA+PB+PC最小值的线段;当B、P、E、D四点共线时,PA+PB+PC值最小,最小值为BD.先由旋转的性质得出△APC≌△DEC,则CP=CE,再证明△PCE是等边三角形,得到PE=CE=CP,然后根据菱形、三角形外角的性质,等腰三角形的判定得出BP=CP,同理,得出DE=CE,则BP=PE=ED=![]() BD.
BD.
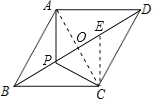
将△APC绕点C顺时针旋转60°,得到△DEC,连接PE、DE,
则线段BD等于PA+PB+PC最小值的线段;
如图,当B. P、E. D四点共线时,PA+PB+PC值最小,最小值为BD.
∵将△APC绕点C顺时针旋转60°,得到△DEC,
∴△APC≌△DEC,
∴CP=CE,∠PCE=60°,
∴△PCE是等边三角形,
∴PE=CE=CP,∠EPC=∠CEP=60°.
∵菱形ABCD中,∠ABP=∠CBP= ![]() ∠ABC=30°,
∠ABC=30°,
∴∠PCB=∠EPC∠CBP=60°∠30°=30°,
∴∠PCB=∠CBP=30°,
∴BP=CP,
同理,DE=CE,
∴BP=PE=ED.
连接AC,交BD于点O,则AC⊥BD.
在Rt△BOC中,∵∠BOC=90°,∠OBC=30°,BC=4,
∴BO=BCcos∠OBC=4×![]() =
= ![]() ,
,
∴BD=2BO=![]() ,
,
∴BP=![]() BD=
BD=![]() .
.
即当PA+PB+PC值最小时PB的长为![]() .
.
故答案为:![]() .
.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案 培优三好生系列答案
培优三好生系列答案科目:初中数学 来源: 题型:
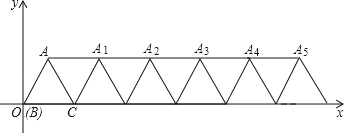
【题目】如图,在平面直角坐标系内,边长为4的等边△ABC的顶点B与原点重合,将△ABC绕顶点C顺时针旋转60°得到△ACA1,将四边形ABCA1看作一个基本图形,将此基本图形不断复制并平移,请回答:
(1)点A的坐标为 ;点A1的坐标为 .
(2)A2018的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某校九年级(3)班的一个学习小组进行测量小山高度的实践活动.部分同学在山脚A点处测得山腰上一点D的仰角为30°,并测得AD的长度为180米.另一部分同学在山顶B点处测得山脚A点的俯角为45°,山腰D点的俯角为60°,请你帮助他们计算出小山的高度BC.(计算过程和结果都不取近似值)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小华是花店的一名花艺师,她每天都要为花店制作普通花束和精致花束,她每月工作20天,每天工作8小时,她的工资由基本工资和提成工资两部分构成,每月的基本工资为l800元,另每制作一束普通花束可提2元,每制作一束精致花束可提5元.她制作两种花束的数量与所用时间的关系见下表:
制作普通花束(束) | 制作精致花束(束) | 所用时间(分钟) |
10 | 25 | 600 |
15 | 30 | 750 |
请根据以上信息,解答下列问题:
(1)小华每制作一束普通花束和每制作一束精致花束分别需要多少分钟?
(2)2019年11月花店老板要求小华本月制作普通花束的总时间![]() 不少于3000分钟且不超过5000分钟,则小华该月收入
不少于3000分钟且不超过5000分钟,则小华该月收入![]() 最多是多少元?此时小华本月制作普通花束和制作精致花束分别是多少束?
最多是多少元?此时小华本月制作普通花束和制作精致花束分别是多少束?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】快车和慢车同时从甲地出发,以各自的速度匀速向乙地行驶,快车到达乙地后停留了45分钟,立即按原路以另一速度匀速返回,直至与慢车相遇.已知慢车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,则快车从乙地返回时的速度为__________千米/时

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是双曲线y=﹣![]() 在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=
在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=![]() 上运动,则k的值为_____.
上运动,则k的值为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com