Question

【题目】是等边三角形，作直线，点关于直线的对称点为，连接，直线交直线于点，连接．

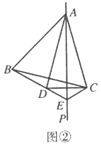
（1）如图①，求证：；（提示：在BE上截取，连接．）

（2）如图②、图③，请直接写出线段，，之间的数量关系，不需要证明；

（3）在（1）、（2）的条件下，若，则__________．

Answer 1

【答案】（1）见解析；（2）图②中，CE+BE=AE，图③中，AE+BE=CE；（3）1.5或4.5

【解析】

（1）在BE上截取，连接，只要证明△AED≌△AFB，进而证出△AFE为等边三角形，得出CE+AE= BF+FE，即可解决问题；

（2）图②中，CE+BE=AE，延长EB到F，使BF=CE，连接，只要证明△ACE≌△AFB，进而证出△AFE为等边三角形，得出CE+BE= BF+BE，即可解决问题；图③中，AE+BE=CE，在EC上截取CF=BE，连接，只要证明△AEB≌△AFC，进而证出△AFE为等边三角形，得出AE+BE =CF+EF，即可解决问题；

（3）根据线段，，，BD之间的数量关系分别列式计算即可解决问题．

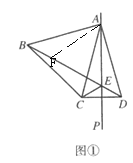
（1）证明：在BE上截取，连接，

在等边△ABC中，
AC=AB，∠BAC=60°
由对称可知：AP是CD的垂直平分线，AC=AD，∠EAC=∠EAD，
设∠EAC=∠DAE=x．
∵AD=AC=AB，
∴∠D=∠ABD=（180°-∠BAC-2x）=60°-x，
∴∠AEB=60-x+x=60°．
∵AC=AB，AC=AD，

∴AB=AD，

∴∠ABF=∠ADE，

∵，

∴△ABF≌△ADE，

∴AF=AE，BF=DE，

∴△AFE为等边三角形，

∴EF=AE，

∵AP是CD的垂直平分线，

∴CE=DE，

∴CE=DE=BF，
∴CE+AE= BF+FE =BE；

（2）图②中，CE+BE=AE，延长EB到F，使BF=CE，连接

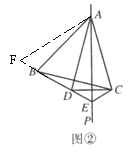
在等边△ABC中，
AC=AB，∠BAC=60°
由对称可知：AP是CD的垂直平分线，AC=AD，∠EAC=∠EAD，
∴AB =AD，CE=DE，

∵AE =AE

∴△ACE≌△ADE，

∴∠ACE=∠ADE

∵AB =AD，

∴∠ABD=∠ADB

∴∠ABF=∠ADE=∠ACE

∵AB=AC，BF=CE，

∴△ACE≌△ABF，

∴AE=AF，∠BAF=∠CAE

∵∠BAC=∠BAE+∠CAE =60°

∴∠EAF=∠BAE+∠BAF =60°

∴△AFE为等边三角形，

∴EF=AE，

∴AE=BE+BF= BE+CE，即CE+BE=AE；

图③中，AE+BE=CE，在EC上截取CF=BE，连接，

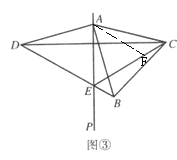
在等边△ABC中，
AC=AB，∠BAC=60°
由对称可知：AP是CD的垂直平分线，AC=AD，∠EAC=∠EAD，
∴AB =AD，CE=DE，

∵AE =AE

∴△ACE≌△ADE，

∴∠ACE=∠ADE

∵AB =AD，

∴∠ABD=∠ADB

∴∠ABD=∠ADE=∠ACE

∵AB=AC，BE=CF，

∴△ACF≌△ABE，

∴AE=AF，∠BAE=∠CAF

∵∠BAC=∠BAF+∠CAF =60°

∴∠EAF=∠BAF+∠BAE =60°

∴△AFE为等边三角形，

∴EF=AE，

∴CE =EF+CF= AE + BE，即AE+BE=CE；

（3）在（1）的条件下，若，则AE=3，

∵CE+AE=BE，

∴BE-CE=3，

∵BD=BE+ED=BE+CE=6，

∴CE=1.5；

在（2）的条件下，若，则AE=3，因为图②中，CE+BE=AE，而BD=BE-DE=BE-CE，所以BD不可能等于2AE；

图③中，若，则AE=3，

∵AE+BE=CE，

∴CE-BE=3，

∵BD=BE+ED=BE+CE=6，

∴CE=4.5．

即CE=1.5或4.5．