
【题目】
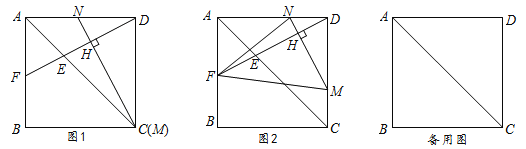
正方形ABCD边长为4 cm,点E,M分别是线段AC,CD上的动点,连接DE并延长,交正方形ABCD的边于点F,过点M作MN⊥DF于H,交AD于N.
(1)如图1,若点M与点C重合,求证:DF=MN;
(2)如图2,若点M从点C出发,以1cm/s的速度沿CD向点D运动,点E同时从点A出发,以![]() cm/s速度沿AC向点C运动,运动时间为t(t>0);
cm/s速度沿AC向点C运动,运动时间为t(t>0);
①当点F是边AB的中点时,求t的值;
②连结FM,FN,当t为何值时△MNF是等腰三角形(直接写出t值).
【答案】(1)证明见解析;(2)t=![]() ;②t=2或t=4.
;②t=2或t=4.
【解析】
试题分析:(1)先判定△ADF≌△DNC,即可得到结论;
(2)①当点F是AB中点时,由比例式![]() ,计算即可,②先表示出AF,DN=CM=t,AN=DM=4-t,再分三种情况计算.
,计算即可,②先表示出AF,DN=CM=t,AN=DM=4-t,再分三种情况计算.
试题解析:(1)证明:∵∠DNC+∠ADF=90°,∠DNC+∠DCN=90°.
∴∠ADF=∠DCN.
在△ADF与△DNC中,

∴△ADF≌△DNC(ASA). 2分
∴DF=MN.
(2)①当点F是边AB中点时,则AF=![]() AB=2.
AB=2.
由题意可知,CM=t,AE=![]() t,CE=4
t,CE=4![]() -
-![]() t
t
∵AB∥CD,
∴△AEF∽△CED.
∴![]() .
.
即![]()
∴t=![]()
②t=2或t=4.
详细解答过程如下:
∵△AEF∽△CED.
∴![]()
∴![]()
∴AF=![]()
易证△MND∽△DFA,
∴![]() ,
,
∴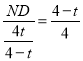 ,解得ND=t.
,解得ND=t.
∴DN=CM=t,AN=DM=4-t
若△MNF为等腰三角形,则可能有三种情形:
(ⅰ) 若FN=FM,由MN⊥DF知,FD为NM的垂直平分线,∴DN=DM
即t=4-t,∴t=2(此时点F与点B重合)
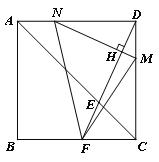
(ⅱ)若FM=MN,显然此时点F在BC边上,如图所示,
由∠NDM=∠MCF,ND=MC,FM=MN
可得△MFC≌△NMD,∴FC=DM=4-t.
由△NDM∽△DCF,可得![]()
∴![]() ,∴t=4(此时点F与点C重合)
,∴t=4(此时点F与点C重合)
(ⅲ)若FN=MN,如图所示,
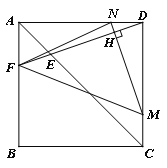
由∠FAN=∠NDM,AN=DM,FN=MN
可得△FAN≌△NDM,∴AF=DN,即![]() =t,
=t,
解得t=0(此时点F与点A重合)
∵t>0,∴不符合题意,∴此种情形不存在.
综上所述,当t=2或t=4时,△MNF能够成为等腰三角形.


科目:初中数学 来源: 题型:
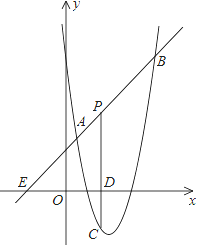
【题目】如图,直线![]() 与抛物线
与抛物线![]() 相交于A(
相交于A(![]() ,
,![]() )和B(4,
)和B(4,![]() ),点P是线段AB上异于A、B的动点,过点P作PC⊥
),点P是线段AB上异于A、B的动点,过点P作PC⊥![]() 轴于点D,交抛物线于点C.
轴于点D,交抛物线于点C.
(1)求抛物线的解析式;
(2)是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;
(3)求△PAC为直角三角形时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学随机调查了15名学生,了解他们一周在校参加课外体育锻炼的时间,列表如表所示:
锻炼时间(小时) | 5 | 6 | 7 | 8 |
人数 | 3 | 7 | 4 | 1 |
则这15名学生一周在校参加课外体育锻炼时的中位数和众数分别是( )
A. 6.5,7B. 7,7C. 6.5,6D. 6,6
查看答案和解析>>
科目:初中数学 来源: 题型:
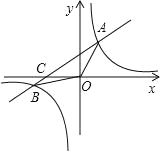
【题目】如图,已知反比例函数y=![]() 与一次函数y=x+b的图象在第一象限相交于点A(1,-k+4).
与一次函数y=x+b的图象在第一象限相交于点A(1,-k+4).
(1)试确定这两个函数的表达式;
(2)求出这两个函数图象的另一个交点B的坐标,并求△A0B的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com