
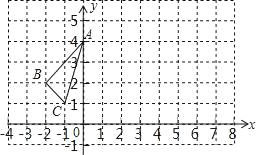
【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)将△ABC向右平移6个单位,作出平移后的△A1B1C1,并写出△A1B1C1各顶点的坐标;
(2)在y轴上是否存在点M,使得CM+BM最小?若存在,求出点M坐标;若不存在,请说明理由.
【答案】(1)A1(6,4),B1(4,2),C1(5,1);(2)(0,![]() )
)
【解析】
(1)分别作出点A,B,C向右平移6个单位得到的对应点,再顺次连接即可得;
(2)作出点C关于y轴的对称点C′,连接C′B,与y轴的交点即为所求,再利用待定系数法求出直线C′B的解析式,求出与y轴的交点即可.
解:(1)如图所示,△A1B1C1即为所求,

由图知A1点的坐标为(6,4),B1点的坐标为(4,2),C1点的坐标为(5,1);
(2)点C(﹣1,1)关于y轴的对称点C′的坐标为(1,1),
设直线C′B的解析式为y=kx+b,
则![]()
解得: 
∴直线C′B的解析式为y=﹣![]() x+
x+![]() ,
,
当x=0时,y=![]() ,
,
∴点M的坐标为(0,![]() ).
).


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
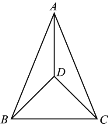
【题目】如图,在△ABC中,AB=AC,D是三角形内一点,连接AD,BD,CD,∠BDC=90°,∠DBC=45°.
(1)求证:∠BAD=∠CAD;
(2)求∠ADB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区为进一步发展基础教育,自![]() 年以来加大了教育经费的投入,
年以来加大了教育经费的投入,![]() 年该地区投入教育经费
年该地区投入教育经费![]() 万元,
万元,![]() 年投入教育经费
年投入教育经费![]() 万元.
万元.
(1)求该地区这两年投入教育经费的年平均增长率;
(2)若该地区教育经费的投入还将保持相同的年平均增长率,请预算![]() 年该地区投入教育经费为 万元.
年该地区投入教育经费为 万元.
查看答案和解析>>
科目:初中数学 来源: 题型:
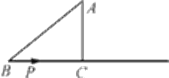
【题目】如图,在Rt△ABC中,∠C=90°,AB=5cm,AC=3cm,动点P从点B出发沿射线BC以1cm/s的速度移动,设运动的时间为ts.
(1)求BC边的长;
(2)当△ABP为直角三角形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,数轴上的点A、B分别表示数a、b,则点A、B(点B在点A的右侧)之间的距离表示为AB=b﹣a,若点C对应的数为c,满足|a+3|+(c﹣9)2=0.
(1)写出AC的值 .
(2)如图②,点D在点C的右侧且距离m(m>0)个单位,点B在线段AC上,满足AB+AC=BD,求AB的值(用含有m的代数式表示).
(3)如图③,若点D在点C的右侧6个单位处,点P从点A出发以2个单位/秒的速度向右运动,同时点M从点C出发以1个单位/秒的速度也向右运动,当到达D点后以原来的速度向相反的方向运动.求经过多长时间,点P和点M之间的距离是2个单位?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中, ![]() 的三个顶点坐标分别为A(2,-4),B(3,-2), C(6,-3).
的三个顶点坐标分别为A(2,-4),B(3,-2), C(6,-3).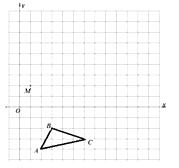
①画出△ABC关于 ![]() 轴对称的△A1B1C1;
轴对称的△A1B1C1;
②以M点为位似中心,在网格中画出△A1B1C1的位似图形△A2B2C2 , 使△A2B2C2与△A1B1C1的相似比为2︰1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】x1、x2、x3、…x20是20个由1,0,﹣1组成的数,且满足:①x1+x2+x3+…+x20=4,②(x1﹣1)2+(x2﹣1)2+(x3﹣1)2…+(x20﹣1)2=32,则这列数中1的个数为_____个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)![]() ÷
÷![]() -
-![]() ×
×![]() +
+![]() ; (2)
; (2)![]() -
-![]() -(
-(![]()
![]() -2
-2![]() );
);
(3)(2-![]() )2017×(2+
)2017×(2+![]() )2016-2
)2016-2![]() -(-
-(-![]() )0 (4)(a+2
)0 (4)(a+2![]() +b)÷(
+b)÷(![]() +
+![]() )-(
)-(![]() -
-![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com