
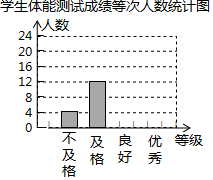
 ijУΪ�˽�ѧ������������Ӹ��꼶�����ȡ����ѧ���������ܲ��ԣ�ÿ��ѧ���IJ��Գɼ�������ӦΪ���㡢���á����������ĸ��ȼ���ͳ��Ա�ڽ��������ݻ��Ƴ�ͼ��ʱ���֣�����©ͳ��4�ˣ�����©ͳ��6�ˣ����Ǽ�ʱ�������Ӷ��γ���ͼͼ�����밴��ȷ���ݽ�����и��⣺
ijУΪ�˽�ѧ������������Ӹ��꼶�����ȡ����ѧ���������ܲ��ԣ�ÿ��ѧ���IJ��Գɼ�������ӦΪ���㡢���á����������ĸ��ȼ���ͳ��Ա�ڽ��������ݻ��Ƴ�ͼ��ʱ���֣�����©ͳ��4�ˣ�����©ͳ��6�ˣ����Ǽ�ʱ�������Ӷ��γ���ͼͼ�����밴��ȷ���ݽ�����и��⣺| ���ܵȼ� | ����ǰ���� | ���������� |
| ���� | 8 | 12 |
| ���� | 16 | 22 |
| ���� | 12 | 12 |
| ������ | 4 | 4 |
| �ϼ� | 40 | 50 |
���� ��1��������Ե���������ȫ���ɣ�
��2�����ݵ���������ݣ���ȫ����ͳ��ͼ���ɣ�
��3�����ݡ����㡱����ռ�İٷֱȣ�����1500���ɵõ������
��� �⣺��1��������£�
| ���ܵȼ� | ����ǰ���� | ���������� |
| ���� | 8 | 12 |
| ���� | 16 | 22 |
| ���� | 12 | 12 |
| ������ | 4 | 4 |
| �ϼ� | 40 | 50 |
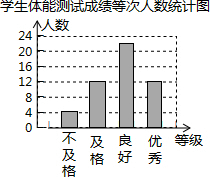
���� ���⿼��������ͳ��ͼ���������������壬�Լ�ͳ�Ʊ���Ū�����е������ǽⱾ��Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
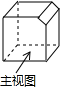 ��ͼ����һ�������屻�е�һ��������õļ����壬����������ͼ�ǣ�������
��ͼ����һ�������屻�е�һ��������õļ����壬����������ͼ�ǣ�������| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
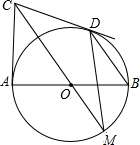 ��ͼ��ABΪ��O��ֱ����CA��CD�ֱ��С�O��A��D��CO���ӳ��߽���O��M����BD��DM��
��ͼ��ABΪ��O��ֱ����CA��CD�ֱ��С�O��A��D��CO���ӳ��߽���O��M����BD��DM���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����C����ABΪֱ���İ�ԲO�����ȷֵ㣬AC=2����ͼ����Ӱ���ֵ�����ǣ�������
��ͼ����C����ABΪֱ���İ�ԲO�����ȷֵ㣬AC=2����ͼ����Ӱ���ֵ�����ǣ�������| A�� | $\frac{4��}{3}$$-\sqrt{3}$ | B�� | $\frac{4��}{3}$-2$\sqrt{3}$ | C�� | $\frac{2��}{3}$$-\sqrt{3}$ | D�� | $\frac{2��}{3}$-$\frac{\sqrt{3}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2��-2 | B�� | -2��$\frac{1}{2}$ | C�� | $\sqrt{3}$��$\frac{\sqrt{3}}{3}$ | D�� | $\sqrt{3}$��-$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\left\{\begin{array}{l}{x=5}\\{y=1}\end{array}\right.$ | B�� | $\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$ | C�� | $\left\{\begin{array}{l}{x=-5}\\{y=-1}\end{array}\right.$ | D�� | $\left\{\begin{array}{l}{x=-4}\\{y=-2}\end{array}\right.$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ֱ������ϵ�У���A��Բ��A������Ϊ��-1��0�����뾶Ϊ1����PΪֱ��y=-$\frac{3}{4}$x+3�ϵĶ��㣬����P����A�����ߣ��е�ΪQ�������߳�PQ����Сֵ��2$\sqrt{2}$��
��ͼ����ֱ������ϵ�У���A��Բ��A������Ϊ��-1��0�����뾶Ϊ1����PΪֱ��y=-$\frac{3}{4}$x+3�ϵĶ��㣬����P����A�����ߣ��е�ΪQ�������߳�PQ����Сֵ��2$\sqrt{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com