
 如图,在直角坐标系中,⊙A的圆心A的坐标为(-1,0),半径为1,点P为直线y=-$\frac{3}{4}$x+3上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是2$\sqrt{2}$.
如图,在直角坐标系中,⊙A的圆心A的坐标为(-1,0),半径为1,点P为直线y=-$\frac{3}{4}$x+3上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是2$\sqrt{2}$. 分析 连接AP,PQ,当AP最小时,PQ最小,当AP⊥直线y=-$\frac{3}{4}$x+3时,PQ最小,根据全等三角形的性质得到AP=3,根据勾股定理即可得到结论.
解答 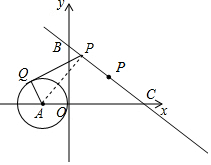 解:如图,作AP⊥直线y=-$\frac{3}{4}$x+3,垂足为P,作⊙A的切线PQ,切点为Q,此时切线长PQ最小∵A的坐标为(-1,0),
解:如图,作AP⊥直线y=-$\frac{3}{4}$x+3,垂足为P,作⊙A的切线PQ,切点为Q,此时切线长PQ最小∵A的坐标为(-1,0),
设直线与x轴,y轴分别交于B,C,
∴B(0,3),C(4,0),
∴OB=3,AC=5,
∴BC=$\sqrt{O{B}^{2}+O{C}^{2}}$=5,
∴AC=BC,
在△APC与△BOC中,$\left\{\begin{array}{l}{∠APC=∠OBC=90°}\\{∠ACB=∠BCO}\\{AC=BC}\end{array}\right.$,
∴△APC≌△OBC,
∴AP=OB=3,
∴PQ=$\sqrt{{3}^{2}-{1}^{2}}$=2$\sqrt{2}$.
点评 本题主要考查切线的性质,掌握过切点的半径与切线垂直是解题的关键,用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:选择题
| A. | (a+b)(b+a) | B. | (a+b)(-a-b) | C. | (a-b)(b-a) | D. | (a-b)(b+a) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在网格(每个小正方形的边长均为1)中选取9个格点(格线的交点称为格点),如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为( )
如图,在网格(每个小正方形的边长均为1)中选取9个格点(格线的交点称为格点),如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为( )| A. | 2$\sqrt{2}$<r<$\sqrt{17}$ | B. | $\sqrt{17}$<r≤3$\sqrt{2}$ | C. | $\sqrt{17}$<r<5 | D. | 5<r<$\sqrt{29}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
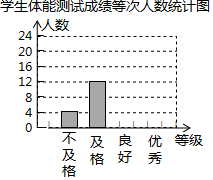 某校为了解学生体质情况,从各年级随机抽取部分学生进行体能测试,每个学生的测试成绩按标准对应为优秀、良好、及格、不及格四个等级,统计员在将测试数据绘制成图表时发现,优秀漏统计4人,良好漏统计6人,于是及时更正,从而形成如图图表,请按正确数据解答下列各题:
某校为了解学生体质情况,从各年级随机抽取部分学生进行体能测试,每个学生的测试成绩按标准对应为优秀、良好、及格、不及格四个等级,统计员在将测试数据绘制成图表时发现,优秀漏统计4人,良好漏统计6人,于是及时更正,从而形成如图图表,请按正确数据解答下列各题:| 体能等级 | 调整前人数 | 调整后人数 |
| 优秀 | 8 | 12 |
| 良好 | 16 | 22 |
| 及格 | 12 | 12 |
| 不及格 | 4 | 4 |
| 合计 | 40 | 50 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
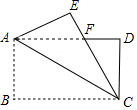 如图,矩形纸片ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点B落在点E处,CE交AD于点F,则DF的长等于( )
如图,矩形纸片ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点B落在点E处,CE交AD于点F,则DF的长等于( )| A. | $\frac{3}{5}$ | B. | $\frac{5}{3}$ | C. | $\frac{7}{3}$ | D. | $\frac{5}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 “赶陀螺”是一项深受人们喜爱的运动,如图所示是一个陀螺的立体结构图.已知底面圆的直径AB=8cm,圆柱体部分的高BC=6cm,圆锥体部分的高CD=3cm,则这个陀螺的表面积是( )
“赶陀螺”是一项深受人们喜爱的运动,如图所示是一个陀螺的立体结构图.已知底面圆的直径AB=8cm,圆柱体部分的高BC=6cm,圆锥体部分的高CD=3cm,则这个陀螺的表面积是( )| A. | 68πcm2 | B. | 74πcm2 | C. | 84πcm2 | D. | 100πcm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
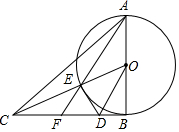 如图,等腰直角△ABC中,∠ABC=90°,以AB为直径作⊙O,连接OC交⊙O于E,AE交BC于点F,过O作OD∥AF交BC于D,连接DE.
如图,等腰直角△ABC中,∠ABC=90°,以AB为直径作⊙O,连接OC交⊙O于E,AE交BC于点F,过O作OD∥AF交BC于D,连接DE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com