
【题目】某校为了解九年级学生的身高情况,随机抽取了部分学生的身高进行调查,利用所得数据绘成如下不完整的统计表和频数分布直方图,根据提供的信息解答下列问题:
身高分组( | 频数 | 百分比 |
| 5 |
|
|
| |
| 15 |
|
| 14 |
|
| 6 |
|
总计 |
|
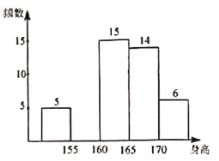
(1)![]() ______.
______.
(2)样本中位数所在组别为______.
(3)通过计算补全频数分布直方图;
(4)该校九年级共有300名学生,估计身高不低于![]() 的学生有多少人.
的学生有多少人.
科目:初中数学 来源: 题型:
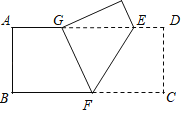
【题目】如图,在长方形纸片ABCD中,AB=3,AD=9,折叠纸片ABCD,使顶点C落在边AD上的点G处,折痕分别交边AD、BC于点E、F,则△GEF的面积最大值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)定义:把四边形的某些边向两方延长,其他各边有不在延长所得直线的同一旁,这样的四边形叫做凹四边形.如图1,四边形![]() 为凹四边形.
为凹四边形.
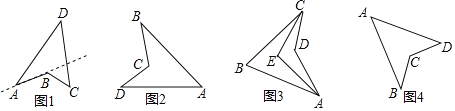
(2)性质探究:请完成凹四边形一个性质的证明.
已知:如图2,四边形![]() 是凹四边形.
是凹四边形.
求证:![]() .
.
(3)性质应用:
如图3,在凹四边形![]() 中,
中,![]() 的角平分线与
的角平分线与![]() 的角平分线交于点
的角平分线交于点![]() ,若
,若![]() ,
,![]() ,则
,则![]() °.
°.
(4)类比学习:
如图4,在凹四边形![]() 中,点
中,点![]() 分别是边
分别是边![]() 的中点,顺次连接各边中点得到四边形
的中点,顺次连接各边中点得到四边形![]() .若
.若![]() ,则四边形
,则四边形![]() 是 .(填写序号即可)
是 .(填写序号即可)
A.梯形 B.菱形 C.矩形 D.正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 为线段
为线段![]() 上一点,
上一点,![]() 为射线
为射线![]() 上一点,且
上一点,且![]() ,连接
,连接![]() .
.
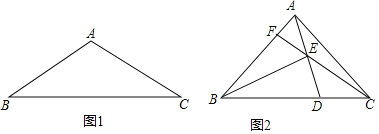
(1)如图1,若![]() ,请补全图形并求
,请补全图形并求![]() 的长;
的长;
(2)如图2,若![]() ,连接
,连接![]() 并延长,交
并延长,交![]() 于点
于点![]() ,小明通过观察、实验提出猜想:
,小明通过观察、实验提出猜想:![]() .小明把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
.小明把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:过![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,先证出
,先证出![]() ,再证出
,再证出![]() 是等腰三角形即可;
是等腰三角形即可;
想法2:过![]() 作
作![]() 交
交![]() 于点
于点![]() ,先证出
,先证出![]() ,再证点
,再证点![]() 为线段
为线段![]() 的中点即可.
的中点即可.
请你参考上面的想法,帮助小明证明![]() .(一种方法即可)
.(一种方法即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
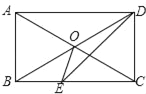
【题目】如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC=90°,对角线AC,BD交于点O,DE平分∠ADC交BC于点E,连接OE.
(1)求证:四边形ABCD是矩形;
(2)若AB=2,求△OEC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十二五”以来,北京市人口增长过快导致城市不堪重负,是造成交通拥堵,能源匮乏等“大城市病”的根源之一.右图是根据北京市统计局近年各年末常住人口增长率及常住人口数的相关数据制作的统计图.

有下面四个判断:①从2011年至2016年,全市常住人口数在逐年下降; ②2010年末全市常住人口数达到近年来的最高值;③2015年末全市常住人口比2014年末增加18.9万人;④从2011年到2016年全市常住人口的年增长率连续递减。其中合理的是( )
A. ①② B. ①④ C. ②③ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与x轴交于点A(1,0),与 y交于点B(0,-2).
与x轴交于点A(1,0),与 y交于点B(0,-2).
(1)求直线AB的表达式;
(2)点C是直线AB上的点,且CA=AB,过动点P(m,0)且垂直于x轴的直线与直线AB 交于点D,若点D不在线段BC上,写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
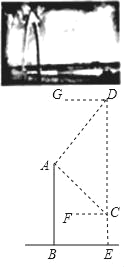
【题目】通达桥即小店汾河桥,是太原新建成的一座跨汾大桥,也是太原首座悬索桥.桥的主塔由曲线形拱门组成,取意“时代之门”.无人机社团的同学计划利用无人机设备测量通达桥拱门的高度.如图,他们先将无人机升至距离桥面50米高的点C处,测得桥的拱门最高点A的仰角∠ACF为30°,再将无人机从C处竖直向上升高200米到点D处,测得点A的俯角∠ADG为45°.已知点A,B,C,D,E在同一平面内,求通达桥拱门最高点A距离桥面BE的高度AB.(结果保留整数,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
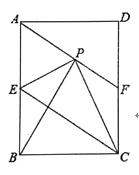
【题目】如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,联结AP并延长AP交CD于F点,
(1)求证:四边形AECF为平行四边形;
(2)如果PA=PC,联结BP,求证:△APB![]() △EPC.
△EPC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com