
分析 (1)先求出$\frac{a+2b}{a-2b}$=±2,再分别代入求出即可;
(2)求出$\sqrt{5}$的范围,求出x、y,再代入求出即可;
(3)根据已知求出a+b=0,ac=1,m=0或1,再分别代入求出即可.
解答 解:(1)∵$|{\frac{a+2b}{a-2b}}$|=2,
∴$\frac{a+2b}{a-2b}$=±2,
当$\frac{a+2b}{a-2b}$=2时,$\frac{a-2b}{a+2b}$=$\frac{1}{2}$,
$\frac{2a+4b}{a-2b}$+$\frac{3a-6b}{a+2b}$-3=2×2+3×$\frac{1}{2}$=5.5;
当$\frac{a+2b}{a-2b}$=-2时,$\frac{a-2b}{a+2b}$=-$\frac{1}{2}$,
$\frac{2a+4b}{a-2b}$+$\frac{3a-6b}{a+2b}$-3=2×(-2)+3×(-$\frac{1}{2}$)=-5.5;
(2)∵2<$\sqrt{5}$<3,
∴12<10+$\sqrt{5}$<13,
∴x=12,y=10+$\sqrt{5}$-12=$\sqrt{5}$-2,
∴x-y=12-($\sqrt{5}$-2)=14-$\sqrt{5}$;
(3)∵a、b互为相反数,a、c互为倒数,并且m的平方等于它的本身,
∴a+b=0,ac=1,m=0或1,
当m=0时,$\frac{2a+2b}{m+2}$+ac=0+1=1;
当m=1时,$\frac{2a+2b}{m+2}$+ac=0+1=1;
即$\frac{2a+2b}{m+2}$+ac=1.
点评 本题考查了估算无理数的大小,绝对值,相反数,倒数,有理数的乘方等知识点,能熟记知识点的内容是解此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
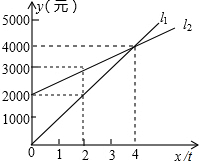 L1反应了某公司产品的销售收入与销售量的关系,L2反应了该公司产品的销售成本与销售量的关系,根据图中信息填空:
L1反应了某公司产品的销售收入与销售量的关系,L2反应了该公司产品的销售成本与销售量的关系,根据图中信息填空:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
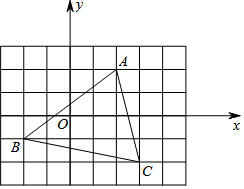 如图,△ABC在平面直角坐标系中:
如图,△ABC在平面直角坐标系中:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
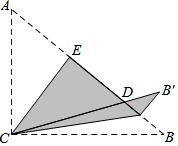 如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B'处,两条折痕与斜边AB分别交于点E、F,则AD=$\frac{18}{5}$;B'F=$\frac{4}{5}$.
如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B'处,两条折痕与斜边AB分别交于点E、F,则AD=$\frac{18}{5}$;B'F=$\frac{4}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
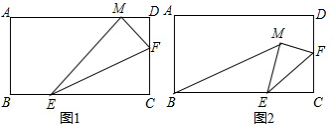
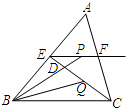 如图所示,在△ABC中,BC=4,E、F分别是AB、AC上的点,且EF∥BC,动点P在射线EF上,BP交CE于点D,∠CBP的平分线交CE于Q,当CQ=$\frac{1}{3}$CE时,EP+BP=8.
如图所示,在△ABC中,BC=4,E、F分别是AB、AC上的点,且EF∥BC,动点P在射线EF上,BP交CE于点D,∠CBP的平分线交CE于Q,当CQ=$\frac{1}{3}$CE时,EP+BP=8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
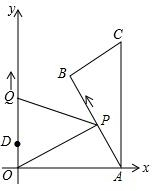 如图,Rt△ABC中,∠B=90°,∠CAB=30°,AC⊥x轴,它的顶点A的坐标为(10,0),C(10,$\frac{20\sqrt{3}}{3}$),点P从点A出发,沿A→B→C的方向匀速运动,同时点Q从点D(0,2)出发,沿y轴正方向以相同速度运动,当点P到达点C时,两点同时停止运动,若P点的速度为2单位/秒,设P运动的时间为t秒.
如图,Rt△ABC中,∠B=90°,∠CAB=30°,AC⊥x轴,它的顶点A的坐标为(10,0),C(10,$\frac{20\sqrt{3}}{3}$),点P从点A出发,沿A→B→C的方向匀速运动,同时点Q从点D(0,2)出发,沿y轴正方向以相同速度运动,当点P到达点C时,两点同时停止运动,若P点的速度为2单位/秒,设P运动的时间为t秒.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com