
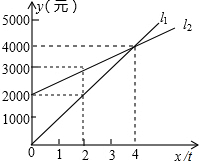
 L1反应了某公司产品的销售收入与销售量的关系,L2反应了该公司产品的销售成本与销售量的关系,根据图中信息填空:
L1反应了某公司产品的销售收入与销售量的关系,L2反应了该公司产品的销售成本与销售量的关系,根据图中信息填空:分析 (1)通过图象观察当x=2时对应的与l2的交点的纵坐标是3000元,与l1的交点是2000元,就可以得出销售收入和销售成本;
(2)通过图象观察当x=6时对应的与l2的交点的纵坐标是3000元,与l1的交点是2000元,就可以得出销售收入和销售成本;
(3)从图象可以看出l1与l2的交点坐标为(4,4000),就有可以求出结论;
(4)从图象可以看出l1与l2的交点坐标为(4,4000),利用函数图象,就有可以求出结论;
(5)设l1的解析式为y1=k1x+b1,l2的解析式为y2=k2x+b2,利用图象上的坐标就可以求出结论.
解答 解:(1)当x=2时对应的与与l1的交点是2000元,l2的交点的纵坐标是3000元;
故答案为:2000,3000;
(2)通过图象观察可以得出,当x=6时,对应的与l1的交点是(6,6000),与l2的交点是(6,5000),
故当销售量为6吨时,销售收入6000元,销售成本为5000元,
故答案为:6000,5000;
(3)从图象观察可以得出:l1与l2的交点坐标是(4,4000),
则当销售量是4吨时,销售成本=销售收入为4000元.
故答案为:4;
(4)从图象观察可以得出:l1与l2的交点坐标是(4,4000),
当销售量x>4时,该公司盈利,当销售量x<4时,该公司亏损;
故答案为:x>4,x<4.
(5)设l1的解析式为y1=k1x,由图象,得
4000=4k1,
解得:k1=1000,
故l1的解析式为:y1=1000x,
设l2的解析式为y2=k2x+b2,由图象,得$\left\{\begin{array}{l}{2000={b}_{2}}\\{4000=4{k}_{2}+{b}_{2}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{2}=500}\\{{b}_{2}=2000}\end{array}\right.$,
故l2的解析式为:y2=500x+2000,
故答案为:y1=1000x,y2=500x+2000.
点评 此题考查了一次函数的应用、运用待定系数法求函数的解析式的运用,识别函数图象和会分析函数图象的能力及一次函数与一元一次方程的结合的运用,搞清楚交点意义和图象的相对位置是关键.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
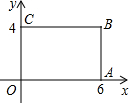 如图,矩形OABC的顶点O在坐标原点,点B的坐标是(6,4),如果矩形OA'B'C'与矩形OABC关于点O位似,且矩形OA'B'C'的面积等于矩形OABC面积的$\frac{1}{9}$,那么点B'的坐标是(2,$\frac{4}{3}$)或(-2,-$\frac{4}{3}$).
如图,矩形OABC的顶点O在坐标原点,点B的坐标是(6,4),如果矩形OA'B'C'与矩形OABC关于点O位似,且矩形OA'B'C'的面积等于矩形OABC面积的$\frac{1}{9}$,那么点B'的坐标是(2,$\frac{4}{3}$)或(-2,-$\frac{4}{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com