9.(1)如图1,已知△ABC中,D是BC的中点,E是AC上一点,$\frac{AE}{EC}$=$\frac{1}{3}$,连结AD与BE相交于点F,求$\frac{AF}{FD}$的值.
小英、小明和小聪各自经过独立思考,分别得到一种添加辅助线的方法从而解决了问题,小明的解法是:
解:过点C作CH∥BE交AD的延长线于点H(如图1-1).
∵CH∥BE,D是BC的中点,
∴$\frac{FH}{FD}$=$\frac{BC}{BD}$=$\frac{2}{1}$.
∵CH∥FE,$\frac{AE}{EC}$=$\frac{1}{3}$,
∴$\frac{AF}{FH}$=$\frac{AE}{EC}$=$\frac{1}{3}$.
∴$\frac{AF}{FD}$=$\frac{AF}{FH}$•$\frac{FH}{FD}$=$\frac{1}{3}$×$\frac{2}{1}$=$\frac{2}{3}$.
小英添加的辅助线是:过点D作DG∥BE交AC于点G(如图1-2);小聪添加的辅助线是:过点A作AM∥BE交CB的延长线于点M(如图1-3);请你在小英和小聪辅助线的添法中选择一种完成解答.
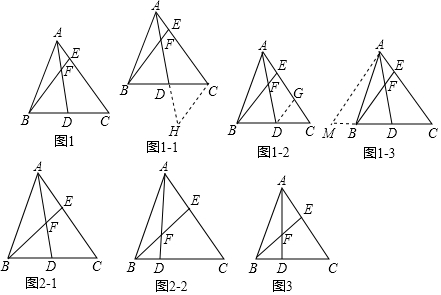
(2)①如图2-1,△ABC中,点D是BC的中点,点E是AC上一点,$\frac{AE}{EC}=\frac{a}{b}$,连结AD与BE相交于点F,则$\frac{AF}{FD}$=$\frac{2a}{b}$(用含a、b的式子表示).
②如图2-2,△ABC中,D、E分别是BC、AC上的点,$\frac{BD}{DC}$=$\frac{m}{n}$,$\frac{AE}{EC}$=$\frac{a}{b}$,连结AD与BE相交于点F,求$\frac{AF}{FD}$的值(用含a、b、m、n的式子表示).
(3)如图3,△ABC中,点D、E分别在BC、AC上,$\frac{BD}{CD}$=$\frac{1}{2}$,$\frac{AE}{EC}$=$\frac{2}{3}$,连结AD与BE相交于点F,已知△ABC的面积为45,求△ABF和四边形CDFE的面积.

 名校课堂系列答案
名校课堂系列答案
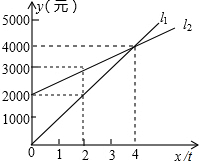 L1反应了某公司产品的销售收入与销售量的关系,L2反应了该公司产品的销售成本与销售量的关系,根据图中信息填空:
L1反应了某公司产品的销售收入与销售量的关系,L2反应了该公司产品的销售成本与销售量的关系,根据图中信息填空: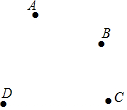 如图所示,平面上有四个点A、B、C、D,根据下列语句画图:
如图所示,平面上有四个点A、B、C、D,根据下列语句画图: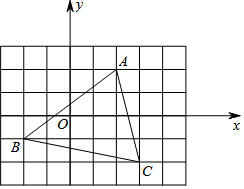 如图,△ABC在平面直角坐标系中:
如图,△ABC在平面直角坐标系中: