
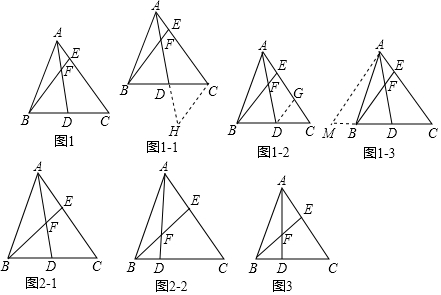
分析 (1)小英的方法只要证明求出AE:EG的值即可解决问题.小聪是方法,只要求出BM:BD的值即可.
(2)①如图2-1中,作DG∥BE交AC于G.想办法求出AE:EG的值即可解决问题.②方法类似①.
(3)如图3中,作DG∥BE交AC于G.首先证明AF:DF=2:1,再分别求出△ABD、△BCE、△ABF、△BDF的面积即可.
解答 (1)解:小英添加的辅助线是:过点D作DG∥BE交AC于点G(如图1-2),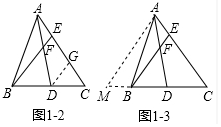
∵DG∥BE,BD=CD,
∴$\frac{CD}{BD}$=$\frac{CG}{EG}$=1,
∴EG=CG,
∵EF∥DG,
∴$\frac{AF}{DF}$=$\frac{AE}{EG}$,
∵$\frac{AE}{EC}$=$\frac{1}{3}$,EG=GC,
∴$\frac{AE}{EG}$=$\frac{2}{3}$,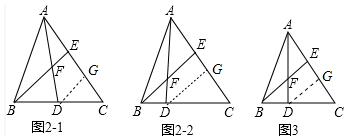
∴$\frac{AF}{DF}$=$\frac{2}{3}$.
小聪添加的辅助线是:过点A作AM∥BE交CB的延长线于点M(如图1-3);
∵AM∥EB,
∴$\frac{BM}{BC}$=$\frac{AE}{EC}$=$\frac{1}{3}$,
∵BD=DC,
∴$\frac{BM}{DB}$=$\frac{2}{3}$,
∵BF∥AM,
∴$\frac{AF}{DF}$=$\frac{BM}{BD}$=$\frac{2}{3}$.
(2)解:①如图2-1中,作DG∥BE交AC于G.
∵DG∥BE,BD=CD,
∴$\frac{CD}{BD}$=$\frac{CG}{EG}$=1,
∴EG=CG,
∵EF∥DG,
∴$\frac{AF}{DF}$=$\frac{AE}{EG}$,
∵$\frac{AE}{EC}$=$\frac{a}{b}$,EG=GC,
∴$\frac{AE}{EG}$=$\frac{2a}{b}$,
∴$\frac{AF}{DF}$=$\frac{2a}{b}$.
故答案为$\frac{2a}{b}$.
②如图2-2中,作DG∥BE交AC于G.
∵DG∥BE,BD=CD,
∴$\frac{BD}{CD}$=$\frac{EG}{CG}$=$\frac{m}{n}$,
∵EF∥DG,
∴$\frac{AF}{DF}$=$\frac{AE}{EG}$,
∵$\frac{AE}{EC}$=$\frac{a}{b}$,设AE=a,EC=b,EG=mk,CG=nk,
则b=mk+nk,k=$\frac{b}{m+n}$
∴EG=$\frac{mb}{m+n}$,
∴$\frac{AE}{EG}$=$\frac{a}{\frac{mb}{m+n}}$=$\frac{a(m+n)}{mb}$
∴$\frac{AF}{DF}$=$\frac{a(m+n)}{mb}$.
(3)解:如图3中,作DG∥BE交AC于G.
∵DG∥BE,
∴$\frac{CD}{BD}$=$\frac{CG}{EG}$=2,
∴2EG=CG,
∵EF∥DG,
∴$\frac{AF}{DF}$=$\frac{AE}{EG}$,
∵$\frac{AE}{EC}$=$\frac{2}{3}$,GC=2EG,
∴$\frac{AE}{EG}$=$\frac{2}{1}$,
∴$\frac{AF}{DF}$=$\frac{2}{1}$,
∵S△ABC=45,BD:DC=1:2,
∴S△ABD=$\frac{1}{3}$×45=15,
∵AF:DF=2:1,
∴S△ABF=$\frac{2}{3}$S△ABD=$\frac{2}{3}$×15=10,
∴S△BDF=5,
∵AE:EC=2:3,
∴S△BEC=$\frac{3}{5}$•S△ABC=$\frac{3}{5}$×45=27,
∴S四边形EFDC=S△ECB-S△BDF=27-5=22.
点评 本题考查相似三角形综合题、平行线分线段成比例定理、三角形的面积等知识,解题的关键是学会添加平行线,利用平行线分线段成比例定理解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{9}{4}$ | B. | $\frac{3}{2}$ | C. | -$\frac{9}{4}$ | D. | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{x}{y}$=$\frac{3}{4}$ | B. | 3y=4x | C. | $\frac{y+x}{y}$=$\frac{7}{4}$ | D. | $\frac{x}{4}$=$\frac{y}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在一长方形休闲广场的四角都设计一块半径相同的四分之一圆的花坛,若圆形的半径为r米,广场长为2a米,宽为b米.
如图,在一长方形休闲广场的四角都设计一块半径相同的四分之一圆的花坛,若圆形的半径为r米,广场长为2a米,宽为b米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com