
 如图,在一长方形休闲广场的四角都设计一块半径相同的四分之一圆的花坛,若圆形的半径为r米,广场长为2a米,宽为b米.
如图,在一长方形休闲广场的四角都设计一块半径相同的四分之一圆的花坛,若圆形的半径为r米,广场长为2a米,宽为b米. 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x+1)(x-1)=x2-1 | B. | x2+2x=x(x+2) | C. | m2+m-4=m(m+1)-4 | D. | 2x2+2x=2x2(1+$\frac{1}{x}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
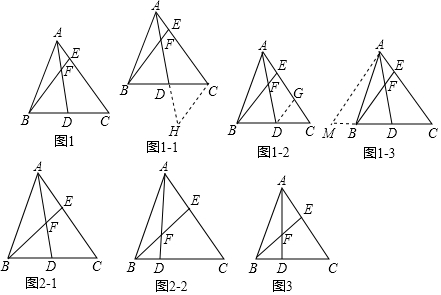
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
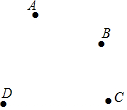 如图所示,平面上有四个点A、B、C、D,根据下列语句画图:
如图所示,平面上有四个点A、B、C、D,根据下列语句画图:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com