
如图1,若△ABC和△ADE为等腰直角三角形,AB=AC,AD=AE,M,N分别EB,CD的中点.

(1)易证:①CD=BE ;②△AMN是 三角形;
(2)当把△ADE绕A点旋转到图2的位置时,

①求证:CD=BE;
②判断△AMN的形状,并证明你的结论;
(3)当△ADE绕A点旋转到图3的位置时,(2)中的结论是否成立?直接写出即可,不要求证明;并求出当AB=2AD时,△ADE与△ABC及△AMN的面积之比.

(1)等腰直角 ;(2)证明见解析;(3)(2)中的结论成立,△ADE与△ABC及△AMN的面积之比为:4:16:5.
【解析】
试题分析:(1)根据已知条件易得△AMN等腰直角三角形;
(2)①用SAS证明△DAC≌△EAB,易得结论;②由于△DAC≌△EAB可以推出△DAM≌△EAN,得到CD=BE,再找角之间的关系易得结论;
(3)(2)中结论成立,令AD=a,求出△ADE与△ABC及△AMN的面积,再求出比值.

试题解析:(1)等腰直角
(2)① ∵ ∠DAE=∠CAB=90°
∴ ∠DAC=∠EAB
又∵ AD=AE AC=AB
∴ △DAC≌△EAB
∴ CD=BE;
②△AMN是等腰直角三角形
∵ △DAC≌△EAB
∴∠CDA=∠BEA
∵ CD=BE
∴ DM=EN
又∵ AD=AE
∴ △DAM≌△EAN
∴ AM=AN,∠DAM =∠EAN
∵ ∠DAM+∠MAE=90°
∴ ∠EAN+∠MAE=90°
∴ ∠MAN=90°
∴△AMN是等腰直角三角形;
(3) 当△ADE绕A点旋转到图3的位置时,(2)中的结论成立(或CD=BE,△AMN是等腰直角三角形)
设AD=a, 那么AC=2a (a≠0)
CD=  a,AM=
a,AM= 
△ADE与△ABC及△AMN的面积之比为: :
: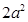 :
: =4:16:5.
=4:16:5.
考点:1.旋转的性质;2.全等三角形的判定与性质;3.等腰直角三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2009年湖南省常德市中考数学试题及答案 题型:059
如图,若△ABC和△ADE为等边三角形,M,N分别EB,CD的中点,易证:CD=BE,△AMN是等边三角形.
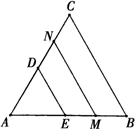
(1)当把△ADE绕A点旋转到如图的位置时,CD=BE是否仍然成立?若成立请证明,若不成立请说明理由;

(2)当△ADE绕A点旋转到如图的位置时,△AMN是否还是等边三角形?若是,请给出证明,并求出当AB=2AD时,△ADE与△ABC及△AMN的面积之比;若不是,请说明理由.

查看答案和解析>>
科目:初中数学 来源:2011—2012学年陕西西安阎良区七年级下期期末数学试卷(带解析) 题型:解答题
四边形ABCD中,∠A=140°,∠D=80°.
(1)如图①,若∠B=∠C,试求出∠C的度数;
(2)如图②,若∠ABC的角平分线交DC于点E,且BE∥AD,试求出∠C的度数;
(3)如图③,若∠ABC和∠BCD的角平分线交于点E,试求出∠BEC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图1若△ABC和△ADE为等边三角形,M,N分别EB,CD的中点,易证:CD=BE,△AMN是等边三角形.
(1)当把△ADE绕A点旋转到图2位置时,CD=BE是否仍然成立?若成立请证明,若不成立请说明理由;
(2)当△ADE绕A点旋转到图3位置时,△AMN是否还是等边三角形?若是,请给出证明,并求出当AB=2AD时,△ADE与△ABC及△AMN的面积之比;若不是,请说明理由.
 |
查看答案和解析>>
科目:初中数学 来源:湖南省中考真题 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com