

| 解:(1)CD=BE;理由如下 ∵△ABC和△ADE为等边三角形, ∴AB=AC,AE=AD,∠BAC=∠EAD=60°, ∵∠BAE=∠BAC-∠EAC=60°-∠EAC, ∠DAC=∠DAE-∠EAC=60°-∠EAC, ∴∠BAE=∠DAC, ∴△ABE≌△ACD, ∴CD=BE; (2)△AMN是等边三角形;理由如下: ∵△ABE≌△ACD, ∴∠ABE=∠ACD, ∵M、N分别是BE、CD的中点, ∴BM=  , ,∵AB=AC,∠ABE=∠ACD, ∴△ABM≌△ACN, ∴AM=AN,∠MAB=∠NAC, ∴∠NAM=∠NAC+∠CAM=∠MAB+∠CAM=∠BAC=60°, ∴△AMN是等边三角形, 设AD=a,则AB=2a, ∵AD=AE=DE,AB=AC, ∴CE=DE, ∵△ADE为等边三角形, ∴∠DEC=120°,∠ADE=60°, ∴∠EDC=∠ECD=30°, ∴∠ADC=90°, ∴在Rt△ADC中,AD=a,∠ACD=30°, ∴CD=  , ,∵N为DC中点, ∴  , ,∴  , ,∵△ADE,△ABC,△AMN为等边三角形, ∴S△ADE∶S△ABC∶S△AMN=  。 。 |
  |


科目:初中数学 来源:2009年湖南省常德市中考数学试题及答案 题型:059
如图,若△ABC和△ADE为等边三角形,M,N分别EB,CD的中点,易证:CD=BE,△AMN是等边三角形.
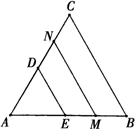
(1)当把△ADE绕A点旋转到如图的位置时,CD=BE是否仍然成立?若成立请证明,若不成立请说明理由;

(2)当△ADE绕A点旋转到如图的位置时,△AMN是否还是等边三角形?若是,请给出证明,并求出当AB=2AD时,△ADE与△ABC及△AMN的面积之比;若不是,请说明理由.

查看答案和解析>>
科目:初中数学 来源:2011—2012学年陕西西安阎良区七年级下期期末数学试卷(带解析) 题型:解答题
四边形ABCD中,∠A=140°,∠D=80°.
(1)如图①,若∠B=∠C,试求出∠C的度数;
(2)如图②,若∠ABC的角平分线交DC于点E,且BE∥AD,试求出∠C的度数;
(3)如图③,若∠ABC和∠BCD的角平分线交于点E,试求出∠BEC的度数.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏盐城市盐都区九年级上学期期末统考数学试卷(解析版) 题型:解答题
如图1,若△ABC和△ADE为等腰直角三角形,AB=AC,AD=AE,M,N分别EB,CD的中点.

(1)易证:①CD=BE ;②△AMN是 三角形;
(2)当把△ADE绕A点旋转到图2的位置时,

①求证:CD=BE;
②判断△AMN的形状,并证明你的结论;
(3)当△ADE绕A点旋转到图3的位置时,(2)中的结论是否成立?直接写出即可,不要求证明;并求出当AB=2AD时,△ADE与△ABC及△AMN的面积之比.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图1若△ABC和△ADE为等边三角形,M,N分别EB,CD的中点,易证:CD=BE,△AMN是等边三角形.
(1)当把△ADE绕A点旋转到图2位置时,CD=BE是否仍然成立?若成立请证明,若不成立请说明理由;
(2)当△ADE绕A点旋转到图3位置时,△AMN是否还是等边三角形?若是,请给出证明,并求出当AB=2AD时,△ADE与△ABC及△AMN的面积之比;若不是,请说明理由.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com