
| A. | 若a>b,则a+c>b+c | B. | 若a+c>b+c,则a>b | C. | 若a>b,则ac2>bc2 | D. | 若ac2>bc2,则a>b |
分析 根据不等式的性质进行判断.
解答 解:A、在不等式a>b的两边同时加上c,不等式仍成立,即a+c>b+c,不符合题意;
B、在不等式a+c>b+c的两边同时减去c,不等式仍成立,即a>b,不符合题意;
C、当c=0时,若a>b,则不等式ac2>bc2不成立,符合题意;
D、在不等式ac2>bc2的两边同时除以不为0的c2,该不等式仍成立,即a>b,不符合题意.
故选:C.
点评 主要考查了不等式的基本性质.“0”是很特殊的一个数,因此,解答不等式的问题时,应密切关注“0”存在与否,以防掉进“0”的陷阱.不等式的基本性质:
(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变.
(2)不等式两边乘(或除以)同一个正数,不等号的方向不变.
(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.


科目:初中数学 来源: 题型:解答题
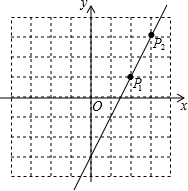 如图,直线l上有一点P1(2,1),将点P1先向右平移1个单位,再向上平移2个单位得到像点P2,点P2恰好在直线l上.
如图,直线l上有一点P1(2,1),将点P1先向右平移1个单位,再向上平移2个单位得到像点P2,点P2恰好在直线l上.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
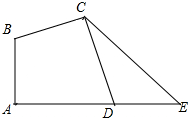 如图,在四边形ABCD中,∠A=∠BCD=90°,BC=DC.延长AD到E点,使DE=AB.
如图,在四边形ABCD中,∠A=∠BCD=90°,BC=DC.延长AD到E点,使DE=AB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
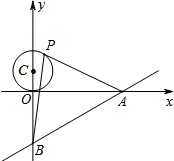 如图,已知直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是( )
如图,已知直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是( )| A. | 8 | B. | 12 | C. | $\frac{21}{2}$ | D. | $\frac{17}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知二次函数y=x2+(1-m)x-m(其中0<m<1)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴为直线l.设P为对称轴l上的点,连接PA、PC,PA=PC
如图,已知二次函数y=x2+(1-m)x-m(其中0<m<1)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴为直线l.设P为对称轴l上的点,连接PA、PC,PA=PC查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com