
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,点G在直径DF的延长线上,∠D=∠G=30°.
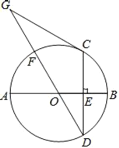
(1)判断CG与圆O的关系,并说明理由;
(2)若CD=6,求线段GF的长度.
【答案】(1)CG是圆O的切线,证明见解析;(2)![]() .
.
【解析】
(1)连接OC,根据三角形内角和定理可得∠DCG=180![]() -∠D-∠G=120
-∠D-∠G=120![]() ,再计算出∠GCO的度数可得OC⊥CG,进而得到CG是⊙O的切线;
,再计算出∠GCO的度数可得OC⊥CG,进而得到CG是⊙O的切线;
(2)设EO=x,则CO=2x,再利用勾股定理计算出EO的长,进而得到CO的长,然后再计算出GF的长即可.
解:
(1)证明:连接OC.
∵OC=OD,∠D=30![]() ,
,
∴∠OCD=∠D=30![]() ,
,
∵∠G=30![]() ,
,
∴∠DCG=180![]() ﹣∠D﹣∠G=120
﹣∠D﹣∠G=120![]() ,
,
∴∠GCO=∠DCG﹣∠OCD=90![]() ,
,
∴OC⊥CG.
又∵OC是⊙O的半径.
∴CG是⊙O的切线.
(2)∵∠D=∠G=30![]() ,
,
∴CG=CD,
∵AB是⊙O的直径,CD⊥AB,
∴CE=![]() CD=3.
CD=3.
∵在Rt△OCE中,∠CEO=90![]() ,∠OCE=30
,∠OCE=30![]() ,
,
∴EO=![]() CO,
CO,![]() ,
,
设EO=x,则CO=2x.
∴(2x)2=x2+32.
解得x=![]() (舍负值).
(舍负值).
∴CO=![]() .
.
∴FO=![]() .
.
在△OCG中,
∵∠OCG=90![]() ,∠G=30
,∠G=30![]() ,
,
∴GO=2CO=![]() .
.
∴GF=GO﹣FO=![]() .
.
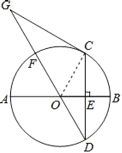


科目:初中数学 来源: 题型:
【题目】矩形![]() 中,线段
中,线段![]() 绕矩形外一点
绕矩形外一点![]() 顺时针旋转,旋转角为
顺时针旋转,旋转角为![]() ,使
,使![]() 点的对应点
点的对应点![]() 落在射线
落在射线![]() 上,
上,![]() 点的对应点
点的对应点![]() 在
在![]() 的延长线上.
的延长线上.
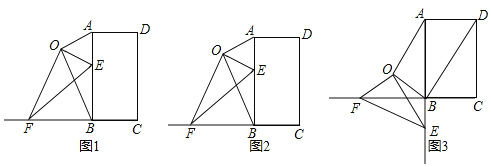
(1)如图1,连接![]() 、
、![]() 、
、![]() 、
、![]() ,则
,则![]() 与
与![]() 的大小关系为______________.
的大小关系为______________.
(2)如图2,当点![]() 位于线段
位于线段![]() 上时,求证:
上时,求证:![]() ;
;
(3)如图3,当点![]() 位于线段
位于线段![]() 的延长线上时,
的延长线上时,![]() ,
,![]() ,求四边形
,求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,以
中,以![]() 为直径作⊙
为直径作⊙![]() ,交
,交![]() 于点
于点![]() ,
,![]() 为弧
为弧![]() 上一点,连接
上一点,连接![]() 、
、![]() 、
、![]() ,交
,交![]() 于点
于点![]() .
.
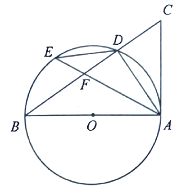
(1)若![]() ,求证:
,求证:![]() 为⊙
为⊙![]() 的切线;
的切线;
(2)若![]() ,求证:
,求证:![]() 平分
平分![]() ;
;
(3)在(2)的条件下,若![]() ,求⊙
,求⊙![]() 的半径.
的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,P1,P2,P3,P4,P5是△DEF边上的5个格点,请按要求完成下列各题:
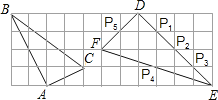
(1)试证明三角形△ABC为直角三角形;
(2)判断△ABC和△DEF是否相似,并说明理由;
(3)画一个三角形,使它的三个顶点为P1,P2,P3,P4,P5中的3个格点并且与△ABC相似(要求:不写作法与证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知菱形ABCD中,AB=5,∠B=60°,⊙A的半径为2,⊙B的半径为3,点E、F分别为⊙A、⊙B上的动点,点P为DC边上的动点,则PE+PF的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代第一部自成体系的数学专著,书中记载:“今有圆材,埋在壁中,不知大小,以锯锯之,深两寸,锯道长八寸,问径几何?”译为:“今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深2寸(ED=2寸),锯道长8寸”,问这块圆形木材的直径是多少?”如图所示,请根据所学知识计算圆形木材的直径AC是( )
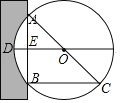
A.5寸B.8寸C.10寸D.12寸
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了保护生态环境,某工厂在一段时间内限产并投入资金进行治污改造.如图描述的是月利润y(万元)和月份x之间的变化关系,治污改造完成前是反比例函数图象的一部分,治污改造完成后是一次函数图象的一部分,则下列说法不正确的是( )

A.5月份该厂的月利润最低
B.治污改造完成后,每月利润比前一个月增加30万元
C.治污改造前后,共有6个月的月利润不超过120万元
D.治污改造完成后的第8个月,该厂月利润达到300万元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为矩形纸片,把纸片ABCD折叠,使点B恰好落在CD边的中点E处, 折痕为AF,若CD=6,则AF等于__________.
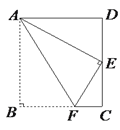
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com