
【题目】如图,C为线段AD上一点,点B为CD的中点,且AD=8cm,BD=2cm.
(1)图中共有多少条线段?
(2)求AC的长.
(3)若点E在直线AD上,且EA=3cm,求BE的长.![]()
【答案】解:(1)图中共有6条线段;
(2)∵点B为CD的中点.
∴CD=2BD.
∵BD=2cm,
∴CD=4cm.
∵AC=AD﹣CD且AD=8cm,CD=4cm,
∴AC=4cm;
(3)当E在点A的左边时,
则BE=BA+EA且BA=6cm,EA=3cm,
∴BE=9cm
当E在点A的右边时,
则BE=AB﹣EA且AB=6cm,EA=3cm,
∴BE=3cm.
【解析】(1)根据线段的定义找出线段即可;
(2)先根据点B为CD的中点,BD=2cm求出线段CD的长,再根据AC=AD﹣CD即可得出结论;
(3)由于不知道E点的位置,故应分E在点A的左边与E在点A的右边两种情况进行解答.
【考点精析】掌握直线、射线、线段和两点间的距离是解答本题的根本,需要知道直线射线与线段,形状相似有关联.直线长短不确定,可向两方无限延.射线仅有一端点,反向延长成直线.线段定长两端点,双向延伸变直线.两点定线是共性,组成图形最常见;同轴两点求距离,大减小数就为之.与轴等距两个点,间距求法亦如此.平面任意两个点,横纵标差先求值.差方相加开平方,距离公式要牢记.


科目:初中数学 来源: 题型:
【题目】如图,点C是线段AB上一点,D是线段CB的中点,已知图中所有的线段的长度之和为23,线段AC的长度与线段CB的长度都是正整数,则线段AC长 . ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
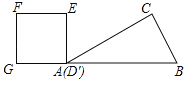
【题目】如图,Rt△ABC中∠C=90°,∠BAC=30°,AB=8,以![]() 为边长的正方形DEFG的一边CD在直线AB上,且点D与点A重合,现将正方形DEFG沿A﹣B的方向以每秒1个单位的速度匀速运动,当点D与点B重合时停止,则在这个运动过程中,正方形DEFG与△ABC的重合部分的面积S与运动时间t之间的函数关系图象大致是( )
为边长的正方形DEFG的一边CD在直线AB上,且点D与点A重合,现将正方形DEFG沿A﹣B的方向以每秒1个单位的速度匀速运动,当点D与点B重合时停止,则在这个运动过程中,正方形DEFG与△ABC的重合部分的面积S与运动时间t之间的函数关系图象大致是( )
A. B.
B.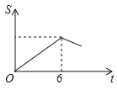 C.
C.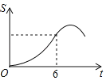 D.
D.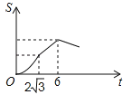
查看答案和解析>>
科目:初中数学 来源: 题型:
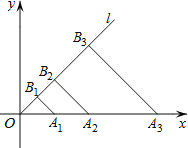
【题目】如图,在平面直角坐标系xOy中,点A1,A2,A3,…,An在x轴的正半轴上,且OA1=2,OA2=2OA1,OA3=2OA2,…,OAn=2OAn﹣1,点B1,B2,B3,…,Bn在第一象限的角平分线l上,且A1B1,A2B2,…,AnBn都与射线l垂直,则B1的坐标是 ,B3的坐标是 ,Bn的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2﹣(2k﹣1)x+k2﹣1=0,其中k<0.
(1)求证:方程有两个不相等的实数根;
(2)当k=﹣1时,求该方程的根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com