
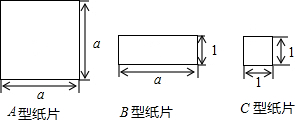
分析 (1)由于1块A型的面积为a2平方厘米,1块B型的面积为a平方厘米,1块C型的面积为1平方厘米,所以A型2块,B型4块,C型4块的总面积为(2a2+4a+4)平方厘米;
(2)把2a2+4a+4减去a2,然后根据完全平方公式得到a2+4a+4=(a+2)2,由此得到正方形的边长;
(3)把2a2+4a+4减去2,然后根据完全平方公式得到2a2+4a+2=2(a+1)2,由此得到正方形的边长,所以从这10块纸板中拿掉2块C类型的纸板满足要求.
解答 解:(1)1块A型的面积为a2平方厘米,1块B型的面积为a平方厘米,1块C型的面积为1平方厘米,所以A型2块,B型4块,C型4块的总面积为(2a2+4a+4)平方厘米;
(2)从这10块纸板中拿掉1块A型纸板,剩下的纸板在不重叠的情况下,可以紧密的排出一个大正方形.剩下纸板的总面积为2a2+4a+4-a2=a2+4a+4,而a2+4a+4=(a+2)2,则此正方形的边长为(a+2)厘米;
(3)从这10块纸板中拿掉2块C类型的纸板,使得剩下的纸板在不重叠的情况下,可以紧密地排出两个相同的大正方形.理由如下:
2a2+4a+4-2=2a2+4a+2=2(a2+2a+1)=2(a+1)2,此时正方形的边长为(a+1)厘米.
点评 本题考查了完全平方公式的几何背景:运用几何直观理解、解决完全平方公式的推导过程,通过几何图形之间的数量关系对完全平方公式做出几何解释.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:解答题
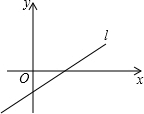 已知直线l:y=(m-3)x+n-2(m,n为常数)的图象如图所示.
已知直线l:y=(m-3)x+n-2(m,n为常数)的图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 物体的质量/kg | 1 | 2 | 3 | 4 |
| 弹簧的长度/cm | 82 | 84 | 86 | 88 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com