练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

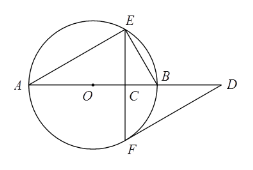
    【题目】如图，是的直径，弦于点，过点作的切线交的延长线于点.

    （1）已知，求的大小（用含的式子表示）；

    （2）取的中点，连接，请补全图形；若，，求的半径.

    【答案】（1）；（2）的半径为2．

    【解析】

    （1）连接，．根据垂径定理以及圆周角定理可得．根据切线的性质有，即可求出的大小.

    （2）根据中位线定理可得，根据平行线的性质有，又，得到，根据勾股定理有．

    设的半径为．，．，代入可得

    ，解方程即可.

    解：（1）连接，．

    ∵，是的直径，

    ∴．

    ∵，，

    ∴．

    ∵为的切线，

    ∴.

    ∴.

    ∴.

    ．

    （2）图形如图所示.连接.

    ∵为的直径，

    ∴为中点， ．

    ∵为的中点，

    ∴，.

    ∵，

    ∴．

    ∵ ，

    ∴.

    ∴．

    设的半径为．

    ∵，，

    ∴.

    ∴．

    ∵，

    ∴.

    解得．（舍去负根）

    ∴的半径为2．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，已知正比例函数y＝x的图象与反比例函数y＝的图象交于A（a，－2），B两点．

    （1）求反比例函数的表达式和点B的坐标；

    （2）P是第一象限内反比例函数图象上一点，过点P作y轴的平行线，交直线AB于点C，连接PO，若△POC的面积为3，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

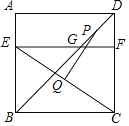
    【题目】如图，正方形ABCD的边长为12，点E在边AB上，BE=8，过点E作EF∥BC，分别交BD、CD于G、F两点．若点P、Q分别为DG、CE的中点，则PQ的长为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商场服装部为了调动营业员的积极性，决定实行目标管理，根据目标完成的情况对营业员进行适当的奖励．为了确定一个适当的月销售目标，商场服装部统计了每位营业员在某月的销售额（单位：万元），数据如下：

    17

    18

    16

    13

    24

    15

    28

    26

    18

    19

    22

    17

    16

    19

    32

    30

    16

    14

    15

    26

    15

    32

    23

    17

    15

    15

    28

    28

    16

    19

    对这30个数据按组距3进行分组，并整理、描述和分析如下．

    频数分布表

    组别

    一

    二

    三

    四

    五

    六

    七

    销售额

    频数

    7

    9

    3

    2

    2

    数据分析表

    平均数

    众数

    中位数

    20.3

    18

    请根据以上信息解答下列问题：

    （1）填空：a=　　，b=　　，c=　　；

    （2）若将月销售额不低于25万元确定为销售目标，则有　　位营业员获得奖励；

    （3）若想让一半左右的营业员都能达到销售目标，你认为月销售额定为多少合适？说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在线教育使学生足不出户也能连接全球优秀的教育资源. 下面的统计图反映了我国在线教育用户规模的变化情况.

    （以上数据摘自《2017年中国在线少儿英语教育白皮书》）

    根据统计图提供的信息，下列推断一定不合理的是

    A. 2015年12月至2017年6月，我国在线教育用户规模逐渐上升

    B. 2015年12月至2017年6月，我国手机在线教育课程用户规模占在线教育用户规模的比例持续上升

    C. 2015年12月至2017年6月，我国手机在线教育课程用户规模的平均值超过7000万

    D. 2017年6月，我国手机在线教育课程用户规模超过在线教育用户规模的70%

    查看答案和解析>>

    科目：初中数学 来源： 题型：

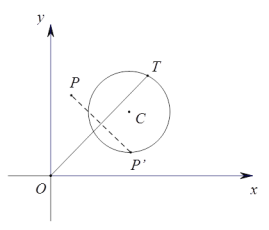
    【题目】在平面直角坐标系中，对于点和，给出如下定义：若上存在一点不与重合，使点关于直线的对称点在上，则称为的反射点．下图为的反射点的示意图．

    （1）已知点的坐标为，的半径为，

    ①在点，，中，的反射点是____________；

    ②点在直线上，若为的反射点，求点的横坐标的取值范围；

    （2）的圆心在轴上，半径为，轴上存在点是的反射点，直接写出圆心的横坐标的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

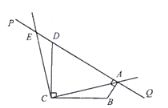
    【题目】如图, ,且,直线经过点.设，于点,将射线绕点按逆时针方向旋转,与直线交于点.

    (1)当时, ；

    (2)求证: ；

    (3)若的外心在其内部,直接写出的取值范围.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点A是反比例函数y=（x＞0）图象上一点，直线y=kx+b过点A并且与两坐标轴分别交于点B，C，过点A作AD⊥x轴，垂足为D，连接DC，若△BOC的面积是4，则△DOC的面积是______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知二次函数的图象与轴交于、两点（点在点的左侧），与轴交于点，且，顶点为．

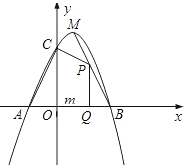
    （1）求二次函数的解析式；

    （2）点为线段上的一个动点，过点作轴的垂线，垂足为，若，四边形的面积为，求关于的函数解析式，并写出的取值范围；

    （3）探索：线段上是否存在点，使为等腰三角形？如果存在，求出点的坐标；如果不存在，请说呀理由．

    查看答案和解析>>

    同步练习册答案