
【题目】如图,已知二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,顶点为
,顶点为![]() .
.
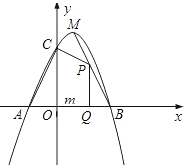
(1)求二次函数的解析式;
(2)点![]() 为线段
为线段![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,垂足为
,垂足为![]() ,若
,若![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数解析式,并写出
的函数解析式,并写出![]() 的取值范围;
的取值范围;
(3)探索:线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 为等腰三角形?如果存在,求出点
为等腰三角形?如果存在,求出点![]() 的坐标;如果不存在,请说呀理由.
的坐标;如果不存在,请说呀理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]() ,
,![]()
![]() .
.
【解析】
(1)可根据OB、OC的长得出B、C两点的坐标,然后用待定系数法即可求出抛物线的解析式.
(2)可将四边形ACPQ分成直角三角形AOC和直角梯形CQPC两部分来求解.先根据抛物线的解析式求出A点的坐标,即可得出三角形AOC直角边OA的长,据此可根据上面得出的四边形的面积计算方法求出S与m的函数关系式.
(3)先根据抛物线的解析式求出M的坐标,进而可得出直线BM的解析式,据此可设出N点的坐标,然后用坐标系中两点间的距离公式分别表示出CM、MN、CN的长,然后分三种情况进行讨论:①CM=MN;②CM=CN;③MN=CN.根据上述三种情况即可得出符合条件的N点的坐标.
解:(1)∵![]() ,∴
,∴![]() ,
,![]() .∴
.∴![]() ,
,
解得![]() ,∴二次函数的解析式为
,∴二次函数的解析式为![]() ;
;
(2)![]() ,
,![]()
设直线![]() 的解析式为
的解析式为![]() ,则有
,则有![]() 解得
解得![]()
∴直线![]() 的解析式为
的解析式为![]()
∵![]() 轴,
轴,![]() ,∴点
,∴点![]() 的坐标为
的坐标为![]()
![]()
![]() ;
;
(3)线段![]() 上存在点
上存在点![]() ,
,![]()
![]() 使
使![]() 为等腰三角形。设
为等腰三角形。设![]() 点坐标为
点坐标为![]() 则:
则:
![]() ,
,![]() ,
,![]()
①当![]() 时
时![]() ,解得
,解得![]() ,
,![]() (舍去)
(舍去)
此时![]()
②当![]() 时,
时,![]() ,
,
解得![]() ,
,![]() (舍去),此时
(舍去),此时![]()
③当![]() 时,
时,![]()
解得![]() ,此时
,此时![]() .
.


科目:初中数学 来源: 题型:
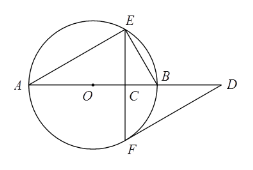
【题目】如图,![]() 是
是![]() 的直径,弦
的直径,弦![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() .
.
(1)已知![]() ,求
,求![]() 的大小(用含
的大小(用含![]() 的式子表示);
的式子表示);
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,请补全图形;若
,请补全图形;若![]() ,
,![]() ,求
,求![]() 的半径.
的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
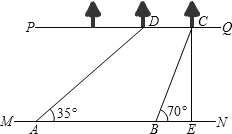
【题目】如图,河流的两岸PQ、MN互相平行,河岸PQ上有一排小树,已知相邻两树之间的距离CD=50米,某人在河岸MN的A处测得∠DAN=35°,然后沿河岸走了120米到达B处,测得∠CBN=70°.求河流的宽度CE(结果保留两个有效数字).(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
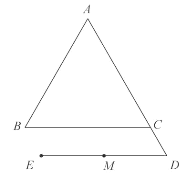
【题目】如图,在等边![]() 中,D为边AC的延长线上一点(
中,D为边AC的延长线上一点(![]() ),平移线段BC,使点C移动到点D,得到线段ED,M为ED的中点,过点M作ED的垂线,交BC于点F,交AC于点G.
),平移线段BC,使点C移动到点D,得到线段ED,M为ED的中点,过点M作ED的垂线,交BC于点F,交AC于点G.
(1)依题意补全图形;
(2)求证:![]() ;
;
(3)连接DF并延长交AB于点H,用等式表示线段AH与CG的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
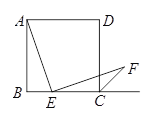
【题目】如图,已知边长为4的正方形ABCD,E是BC边上一动点(与B、C不重合),连结AE,作EF⊥AE交∠BCD的外角平分线于F,设BE=x,△ECF的面积为y,下列图象中,能表示y与x的函数关系的图象大致是( )
A. 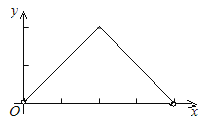 B.
B. 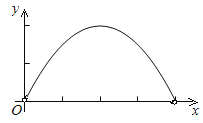
C. 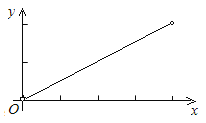 D.
D. 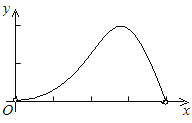
查看答案和解析>>
科目:初中数学 来源: 题型:
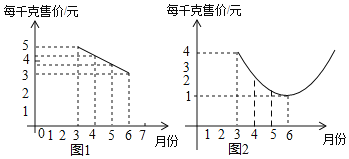
【题目】某种蔬菜的销售单价y1与销售月份x之间的关系如图1所示,成本y2与销售月份x之间的关系如图2所示(图1的图象是线段,图2的图象是抛物线)
(1)已知6月份这种蔬菜的成本最低,此时出售每千克的收益是多少元?(收益=售价﹣成本)
(2)哪个月出售这种蔬菜,每千克的收益最大?简单说明理由.
(3)已知市场部销售该种蔬菜4、5两个月的总收益为22万元,且5月份的销售量比4月份的销售量多2万千克,求4、5两个月的销售量分别是多少万千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
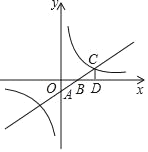
【题目】如图,一次函数y=kx+b的图象与坐标轴分别交于A、B两点,与反比例函数y=![]() 的图象在第一象限的交点为C,CD⊥x轴于D,若OB=3,OD=6,△AOB的面积为3.
的图象在第一象限的交点为C,CD⊥x轴于D,若OB=3,OD=6,△AOB的面积为3.
(1)求一次函数与反比例函数的表达式;
(2)当x>0时,比较kx+b与![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2+bx+2﹣b在自变量x的值满足﹣1≤x≤2的情况下,若对应的函数值y的最大值为6,则b的值为( )
A. ﹣1或2B. 2或6C. ﹣1或4D. ﹣2.5或8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com