练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

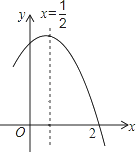
    如图是二次函数y=ax2+bx+c（a≠0）图象的一部分，对称轴为x=，且经过点（2，0），有下列说法：①abc＜0；②a+b=0；③4a+2b+c＜0；④若（0，y1），（1，y2）是抛物线上的两点，则y1=y2．上述说法正确的是（　　）

    　

    A．

    ①②④

    B．

    ③④

    C．

    ①③④

    D．

    ①②

     


    A解：①∵二次函数的图象开口向下，

    ∴a＜0，

    ∵二次函数的图象交y轴的正半轴于一点，

    ∴c＞0，

    ∵对称轴是直线x=，

    ∴﹣，

    ∴b=﹣a＞0，

    ∴abc＜0．

    故①正确；

    ②∵由①中知b=﹣a，

    ∴a+b=0，

    故②正确；

    ③把x=2代入y=ax2+bx+c得：y=4a+2b+c，

    ∵抛物线经过点（2，0），

    ∴当x=2时，y=0，即4a+2b+c=0．

    故③错误；

    ④∵（0，y1）关于直线x=的对称点的坐标是（1，y1），

    ∴y1=y2．

    故④正确；

    综上所述，正确的结论是①②④．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    先化简，再求值：÷（﹣1），其中x=2﹣．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    定义[x]为不超过x的最大整数，如[3.6]=3，[0.6]=0，[﹣3.6]=﹣4．对于任意实数x，下列式子中错误的是（　　）

    　

    A．

    [x]=x（x为整数）

    B．

    0≤x﹣[x]＜1

    　

    C．

    [x+y]≤[x]+[y]

    D．

    [n+x]=n+[x]（n为整数）

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    问题探究：

    （一）新知学习：

    圆内接四边形的判断定理：如果四边形对角互补，那么这个四边形内接于圆（即如果四边形EFGH的对角互补，那么四边形EFGH的四个顶点E、F、G、H都在同个圆上）．

    （二）问题解决：

    已知⊙O的半径为2，AB，CD是⊙O的直径．P是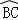上任意一点，过点P分别作AB，CD的垂线，垂足分别为N，M．

    （1）若直径AB⊥CD，对于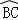上任意一点P（不与B、C重合）（如图一），证明四边形PMON内接于圆，并求此圆直径的长；

    （2）若直径AB⊥CD，在点P（不与B、C重合）从B运动到C的过程汇总，证明MN的长为定值，并求其定值；

    （3）若直径AB与CD相交成120°角．

    ①当点P运动到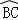的中点P1时（如图二），求MN的长；

    ②当点P（不与B、C重合）从B运动到C的过程中（如图三），证明MN的长为定值．

    （4）试问当直径AB与CD相交成多少度角时，MN的长取最大值，并写出其最大值．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，边长为a，b的矩形的周长为14，面积为10，则a2b+ab2的值为（　　）

    　

    A．

    140

    B．

    70

    C．

    35

    D．

    24

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，直线y=2x+4与x，y轴分别交于A，B两点，以OB为边在y轴右侧作等边三角形OBC，将点C向左平移，使其对应点C′恰好落在直线AB上，则点C′的坐标为　　．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在△ABC中，∠ABC=90°，以AB的中点O为圆心、OA为半径的圆交AC于点D，E是BC的中点，连接DE，OE．

    （1）判断DE与⊙O的位置关系，并说明理由；

    （2）求证：BC2=CD•2OE；

    （3）若cos∠BAD=，BE=6，求OE的长．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    计算：×（﹣）+|﹣2|+（）﹣3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    晋商大院的许多窗格图案蕴含着对称之美，现从中选取以下四种窗格图案，其中是中心对称图形但不是轴对称图形的是（　　）

    　

    A．

    B．

    C．

    D．

    　

       

    查看答案和解析>>

    同步练习册答案