
问题探究:
(一)新知学习:
圆内接四边形的判断定理:如果四边形对角互补,那么这个四边形内接于圆(即如果四边形EFGH的对角互补,那么四边形EFGH的四个顶点E、F、G、H都在同个圆上).
(二)问题解决:
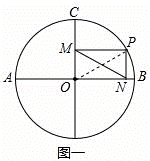
已知⊙O的半径为2,AB,CD是⊙O的直径.P是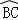 上任意一点,过点P分别作AB,CD的垂线,垂足分别为N,M.
上任意一点,过点P分别作AB,CD的垂线,垂足分别为N,M.
(1)若直径AB⊥CD,对于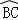 上任意一点P(不与B、C重合)(如图一),证明四边形PMON内接于圆,并求此圆直径的长;
上任意一点P(不与B、C重合)(如图一),证明四边形PMON内接于圆,并求此圆直径的长;
(2)若直径AB⊥CD,在点P(不与B、C重合)从B运动到C的过程汇总,证明MN的长为定值,并求其定值;
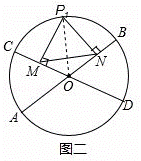
(3)若直径AB与CD相交成120°角.
①当点P运动到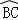 的中点P1时(如图二),求MN的长;
的中点P1时(如图二),求MN的长;
②当点P(不与B、C重合)从B运动到C的过程中(如图三),证明MN的长为定值.
(4)试问当直径AB与CD相交成多少度角时,MN的长取最大值,并写出其最大值.

解:(1)如图一,
∵PM⊥OC,PN⊥OB,
∴∠PMO=∠PNO=90°,
∴∠PMO+∠PNO=180°,
∴四边形PMON内接于圆,直径OP=2;
(2)如图一,
∵AB⊥OC,即∠BOC=90°,
∴∠BOC=∠PMO=∠PNO=90°,
∴四边形PMON是矩形,
∴MN=OP=2,
∴MN的长为定值,该定值为2;
(3)①如图二,
∵P1是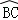 的中点,∠BOC=120°
的中点,∠BOC=120°
∴∠COP1=∠BOP1=60°,∠MP1N=60°.
∵P1M⊥OC,P1N⊥OB,
∴P1M=P1N,
∴△P1MN是等边三角形,
∴MN=P1M.
∵P1M=OP1•sin∠MOP1=2×sin60°= ,
,
∴MN= ;
;
②设四边形PMON的外接圆为⊙O′,连接NO′并延长,
交⊙O′于点Q,连接QM,如图三,
则有∠QMN=90°,∠MQN=∠MPN=60°,
在Rt△QMN中,sin∠MQN= ,
,
∴MN=QN•sin∠MQN,
∴MN=OP•sin∠MQN=2×sin60°=2×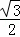 =
= ,
,
∴MN是定值.
(4)由(3)②得MN=OP•sin∠MQN=2sin∠MQN.
当直径AB与CD相交成90°角时,∠MQN=180°﹣90°=90°,MN取得最大值2.



科目:初中数学 来源: 题型:
全民健身和医疗保健是社会普遍关注的问题,2014年,某社区共投入30万元用于购买健身器材和药品.
(1)若2014年社区购买健身器材的费用不超过总投入的 ,问2014年最低投入多少万元购买药品?
,问2014年最低投入多少万元购买药品?
(2)2015年,该社区购买健身器材的费用比上一年增加50%,购买药品的费用比上一年减少 ,但社区在这两方面的总投入仍与2014年相同.
,但社区在这两方面的总投入仍与2014年相同.
①求2014年社区购买药品的总费用;
②据统计,2014年该社区积极健身的家庭达到200户,社区用于这些家庭的药品费用明显减少,只占当年购买药品总费用的 ,与2014年相比,如果2015年社区内健身家庭户数增加的百分比与平均每户健身家庭的药品费用降低的百分比相同,那么,2015年该社区用于健身家庭的药品费用就是当年购买健身器材费用的
,与2014年相比,如果2015年社区内健身家庭户数增加的百分比与平均每户健身家庭的药品费用降低的百分比相同,那么,2015年该社区用于健身家庭的药品费用就是当年购买健身器材费用的 ,求2015年该社区健身家庭的户数.
,求2015年该社区健身家庭的户数.
查看答案和解析>>
科目:初中数学 来源: 题型:
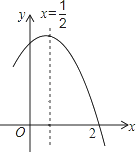
如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x= ,且经过点(2,0),有下列说法:
,且经过点(2,0),有下列说法: ①abc<0;②a+b=0;③4a+2b+c<0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2.上述说法正确的是( )
①abc<0;②a+b=0;③4a+2b+c<0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2.上述说法正确的是( )
|
| A. | ①②④ | B. | ③④ | C. | ①③④ | D. | ①② |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,AB∥CD,直线EF分别交直线AB,CD于点E,F.若∠1=46°30′,则∠1的度数为( )
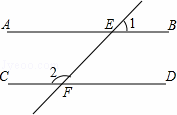
|
| A. | 43°30′ | B. | 53°30′ | C. | 133°30′ | D. | 153°30′ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com